
题目列表(包括答案和解析)
1. 已知集合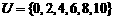 ,
,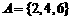 ,则
,则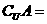
A.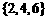 B.
B.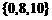 C.
C.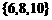 D.
D.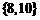
21、(本题满分14分)已知椭圆的两个焦点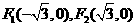 ,且椭圆短轴的两个端点与
,且椭圆短轴的两个端点与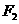 构成正三角形.
构成正三角形.
(1)求椭圆的方程;
(2)过点(1,0)且与坐标轴不平行的直线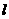 与椭圆交于不同两点P、Q,若在
与椭圆交于不同两点P、Q,若在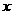 轴上存在定点E(
轴上存在定点E( ,0),使
,0),使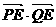 恒为定值,求
恒为定值,求 的值.
的值.
20、(本题满分13分)已知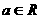 ,函数
,函数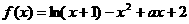 .
.
(1) 若函数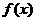 在
在 上为减函数,求实数
上为减函数,求实数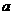 的取值范围;
的取值范围;
(2) 令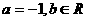 ,已知函数
,已知函数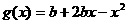 .若对任意
.若对任意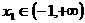 ,总存在
,总存在
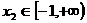 ,使得
,使得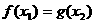 成立,求实数
成立,求实数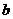 的取值范围.
的取值范围.
19、(本题满分12分)已知数列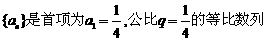 ,
,
设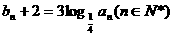 ,数列
,数列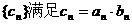 。
。

18、(本题满分12分)如图,在三棱锥P-ABC中,⊿PAB是等边三角形,D,E分别为AB,
PC的中点.
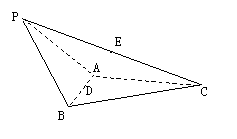 (1)在BC边上是否存在一点F,使得PB∥平面DEF.
(1)在BC边上是否存在一点F,使得PB∥平面DEF.
(2)若∠PAC=∠PBC=90º,证明:AB⊥PC
(3)在(2)的条件下,若AB=2,AC=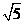 ,求三棱
,求三棱
锥P-ABC的体积
17、(本题满分12分)对甲、乙两种商品的重量的误差进行抽查,测得数据如下(单位:
 ):
):
甲:13 15 14 14 9 14 21 9 10 11
乙:10 14 9 12 15 14 11 19 22 16
(1)画出样本数据的茎叶图,并指出甲,乙两种商品重量误差的中位数;
(2)计算甲种商品重量误差的样本方差;
(3)现从重量误差不低于15的乙种商品中随机抽取两件,求重量误差为19的商品被抽
中的概率。
16、(本题满分12分)已知向量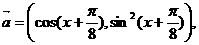
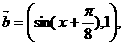 函数
函数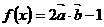
(1)求函数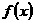 的解析式,并写出函数
的解析式,并写出函数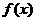 图象的对称中心坐标与对称轴方程.
图象的对称中心坐标与对称轴方程.
(2)求函数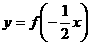 的单调递增区间;
的单调递增区间;
15、已知函数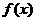 满足
满足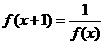 ,且
,且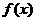 是偶函数, 当
是偶函数, 当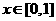 时,
时,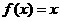 ,若在区间
,若在区间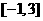 内,函数
内,函数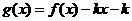 有4个零点,则实数
有4个零点,则实数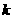 的取值范围是 。
的取值范围是 。
14、在平面内,三角形的面积为S,周长为C,则它的内切圆的半径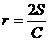 .在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=___________。
.在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=___________。
13、不等式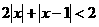 的解集是______________
的解集是______________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com