
题目列表(包括答案和解析)
20.(本小题满分14分)
已知函数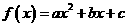
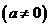 满足
满足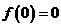 ,对于任意
,对于任意 R都有
R都有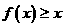 ,且
,且
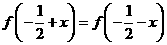 ,令
,令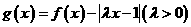 .
.
(1) 求函数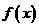 的表达式;
的表达式;
(2) 求函数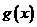 的单调区间;
的单调区间;
(3) 研究函数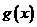 在区间
在区间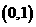 上的零点个数.
上的零点个数.
19.(本小题满分14分)
已知直线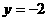 上有一个动点
上有一个动点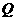 ,过点
,过点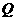 作直线
作直线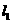 垂直于
垂直于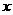 轴,动点
轴,动点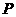 在
在 上,且满足
上,且满足
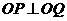 (
( 为坐标原点),记点
为坐标原点),记点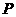 的轨迹为
的轨迹为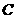 .
.
(1) 求曲线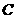 的方程;
的方程;
(2) 若直线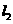 是曲线
是曲线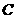 的一条切线, 当点
的一条切线, 当点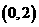 到直线
到直线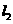 的距离最短时,求直线
的距离最短时,求直线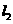 的方程.
的方程.
18.(本小题满分14分)
如图5,在三棱柱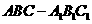 中,侧棱
中,侧棱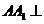 底面
底面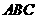 ,
,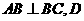 为
为 的中点,
的中点,
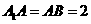 .
.
(1) 求证: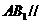 平面
平面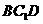 ;
;
(2) 若四棱锥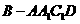 的体积为
的体积为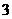 , 求二面角
, 求二面角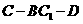 的正切值.
的正切值.
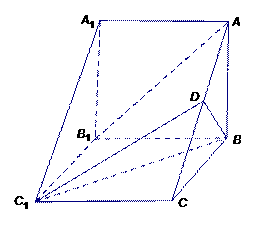
图5
17.(本小题满分12分)
某企业生产的一批产品中有一、二、三等品及次品共四个等级,1件不同等级产品的利润
(单位:元)如表1,从这批产品中随机抽取出1件产品,该件产品为不同等级的概率如表2.
若从这批产品中随机抽取出的1件产品的平均利润(即数学期望)为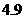 元.
元.
|
等级 |
一等品 |
二等品 |
三等品 |
次品 |
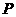 |
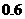 |
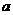 |
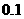 |
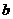 |
|
等级 |
一等品 |
二等品 |
三等品 |
次品 |
|
利润 |
 |
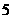 |
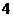 |
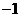 |
表1 表2
(1) 求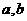 的值;
的值;
(2) 从这批产品中随机取出3件产品,求这3件产品的总利润不低于17元的概率.
16.(本小题满分12分)
已知函数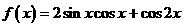 (
( R).
R).
(1) 当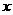 取什么值时,函数
取什么值时,函数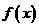 取得最大值,并求其最大值;
取得最大值,并求其最大值;
(2) 若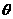 为锐角,且
为锐角,且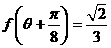 ,求
,求 的值.
的值.
(一)必做题(9-13题)
9.为了了解某地居民月均用电的基本情况, 抽
取出该地区若干户居民的用电数据, 得到频
率分布直方图如图3所示, 若月均用电量在
区间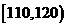 上共有150户, 则月均用电
上共有150户, 则月均用电
量在区间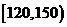 上的居民共有
户.
上的居民共有
户.
10. 以抛物线 上的一点
上的一点 为圆心作圆,若该圆经过抛物线
为圆心作圆,若该圆经过抛物线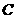 的顶点和焦点,
的顶点和焦点,
那么该圆的方程为 .
11. 已知数列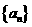 是等差数列, 若
是等差数列, 若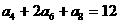 , 则该数列前11项的和为
.
, 则该数列前11项的和为
.
12. △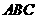 的三个内角
的三个内角 、
、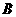 、
、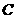 所对边的长分别为
所对边的长分别为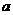 、
、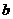 、
、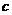 ,已知
,已知
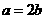 ,
,
则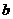 的值为
.
的值为
.
13. 某所学校计划招聘男教师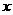 名,女教师
名,女教师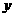 名,
名, 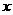 和
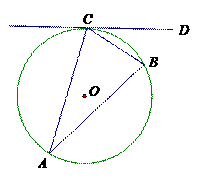
和 须满足约束条件
须满足约束条件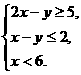
则该校招聘的教师最多是 名.
 (二)选做题(14-15题,考生只能从中选做一题)
(二)选做题(14-15题,考生只能从中选做一题)
14. (几何证明选讲选做题) 如图4, 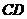 是圆
是圆 的切线, 切点为
的切线, 切点为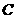 ,
,
点 、
、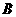 在圆
在圆 上,
上,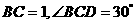 ,则圆
,则圆 的面积为
.
的面积为
.
15. (坐标系与参数方程选讲选做题) 在极坐标系中,若过点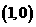 且与
且与
极轴垂直的直线交曲线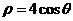 于
于 、
、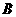 两点,则
两点,则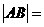 .
.
图4
8. 如图2所示,已知正方体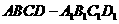 的棱长为2, 长
的棱长为2, 长
 为2的线段
为2的线段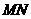 的一个端点
的一个端点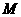 在棱
在棱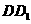 上运动, 另一端点
上运动, 另一端点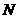
在正方形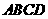 内运动, 则
内运动, 则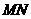 的中点的轨迹的面积为
的中点的轨迹的面积为
A.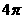 B.
B.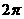
C.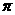 D.
D.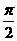
图2
7. 将18个参加青少年科技创新大赛的名额分配给3所学校, 要求每校
至少有一个名额且各校分配的名额互不相等, 则不同的分配方法种数为
A.96 B.114
C.128 D.136
图1
6. “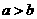 ”
是“
”
是“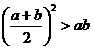 ”成立的
”成立的
A.充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com