
题目列表(包括答案和解析)
7.计算: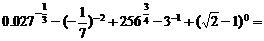 .
.
6.设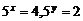 ,则
,则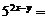 .
.
5.方程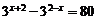 的解是( )
的解是( )
A.2 B.2或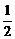 C.2或-2 D.2或
C.2或-2 D.2或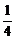
4.以下各式的化简中正确的是( )
A.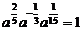 B.
B.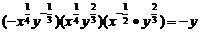
C.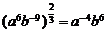 D.
D.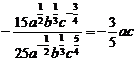
3.下列各式①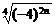 ;②
;②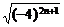 ;③
;③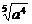 ;④
;④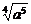 (各式的
(各式的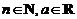 )中,有意义的是( )
)中,有意义的是( )
A.①② B.①③ C.①②③④ D.①③④
2.把根式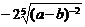 改写成分数指数幂的形式为( )
改写成分数指数幂的形式为( )
A.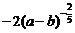 B.
B.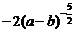
C.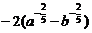 D.
D.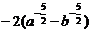
1.下列命题中正确的个数为( )
①-3是81的四次方根; ②正数的n次方根有两个;
③a的n次方根就是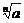 ; ④
; ④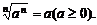
A.1个 B.2个 C.3个 D.4个
[考题1]计算下列各式的值。
(1)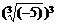 ;(2)
;(2)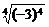 ;(3)
;(3)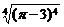 ;
;
(4)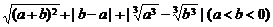 ;
;
(5)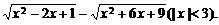
[解析](1)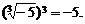
(2)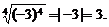
(3)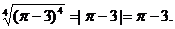
(4)原式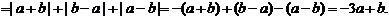
(5)原式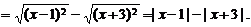
∵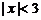 ,∴
,∴
当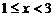 时,原式
时,原式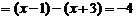 ;
;
当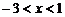 时,原式
时,原式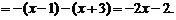
[点评]当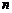 为奇数时,
为奇数时,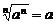 ;
;
当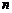 为偶数时,
为偶数时,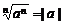 而不是
而不是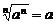 ,这是大于易错的地方,请留心注意。
,这是大于易错的地方,请留心注意。
[考题2]化简下列各式:
(1)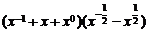 ;
;
(2)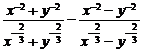 ;
;
(3)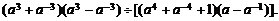
[解析](1)原式=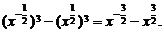
(2)原式=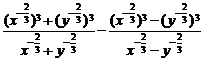
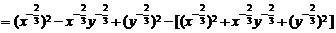
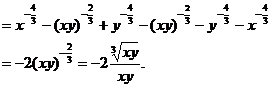
(3)原式=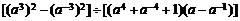
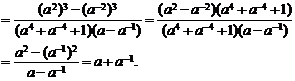
[点评]在进行幂和根式的化简时,一般是先将根式化成幂的形式,并化小数指数幂为分数指数幂,尽可能地统一成分数指数幂形式,再利用幂的运算性质进行化简。还要注意平方差、立方和、立方差公式的应用。
[考题3]判断下列命题的真假:
(1)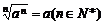 ; (2)
; (2)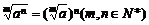 ;
;
(3)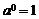 ; (4)
; (4)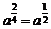 ;
;
(5)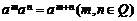 (6)
(6)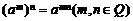
(7)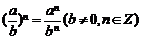 ; (8)
; (8)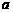 的
的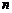 次方次根是
次方次根是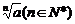 .
.
[分析]判断命题的真假,主要考查命题成立的条件,因此,要对照有关的定义和性质,全面考虑定义和性质的特点,牢记使用范围,才能作出判断。
[解析](1)中是开方问题,当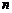 为正奇数时,
为正奇数时,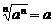 ;当
;当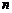 为正偶数时,
为正偶数时,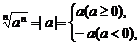 因此(1)错误。
因此(1)错误。
(2)中当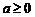 时正确,当
时正确,当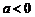 时不一定成立。例如
时不一定成立。例如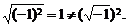
(3)中当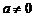 时正确,当
时正确,当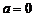 时,
时,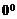 无意义。
无意义。
(4)不成立,例如:取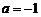 ,则
,则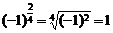 ,但
,但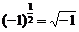 无意义。
无意义。
(5)只有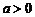 时命题正确,当
时命题正确,当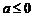 时命题不一定成立。例如:
时命题不一定成立。例如: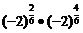
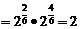 ,而
,而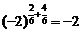 ,∴
,∴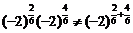 ,本例题中的命题错误。
,本例题中的命题错误。
(6)只有在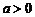 时正确,
时正确,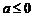 时不一定成立。例如:
时不一定成立。例如: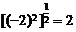 ,
,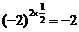 ,则两式不相等。
,则两式不相等。
(7)不妨取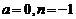 ,则命题不成立。
,则命题不成立。
(8)不妨取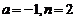 ,则
,则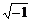 无意义。
无意义。
由以上可知,题中给出的8个命题都是假命题。
[点评](1)要说明一个命题是假命题,只要举出一个反例即可。
(2)注意课本内容的讲授,在“根式”部分,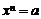 中的
中的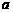 ,根据不同情况,可以取负值,但在“分数指数幂”部分,
,根据不同情况,可以取负值,但在“分数指数幂”部分,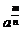 中的
中的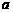 必须取正数,在这部分的概念和性质中,都有
必须取正数,在这部分的概念和性质中,都有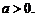
[考题4]计算:(1)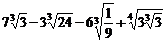 ;
;
(2)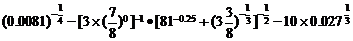 ;
;
(3)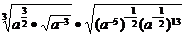 ;
;
(4)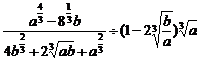 ;
;
(5)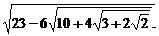
[解析](1)原式=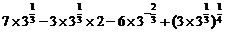
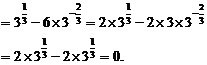
(2)原式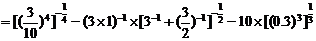
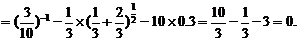
(3)原式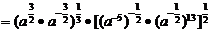
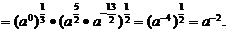
(4)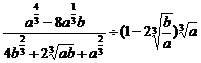
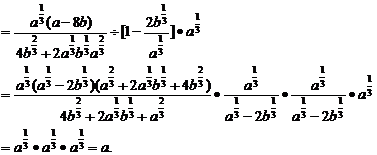
(5)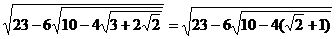
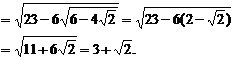
[点评]根式的运算一般都转换成分数指数计算,当式子中含有根式与分数指数幂时应统一为分数指数幂进行计算,当根式中是具体数字时,要考虑运用配方计算,如句子(5)。
[考题5](1)已知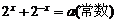 ,求
,求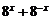 的值;
的值;
(2)已知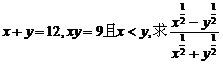 的值。
的值。
[解析](1)∵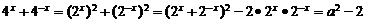 ,
,
∴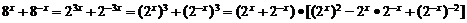
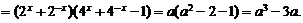
(2)∵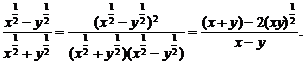 ①
①
又∵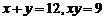 ②
②
∵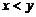 ,∴
,∴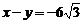 , ③
, ③
将式②③代入式①得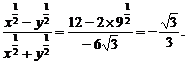
[考题6]设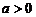 ,且
,且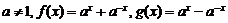 ,且
,且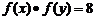 ,
,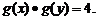
(1)求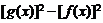 的值;
的值;
(2)求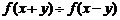 的值;
的值;
(3)求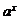 及
及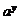 的值。
的值。
[解析](1)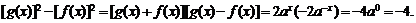
(2)∵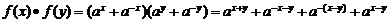
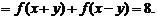 ①
①
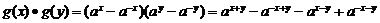
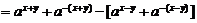
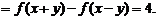 ②
②
由①②联立,解得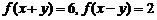 ,
,
∴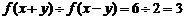 .
.
(3)由②得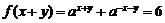 , ③
, ③
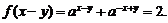 ④
④
令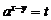 ,则
,则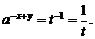
从而由④得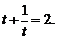 由
由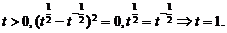
故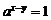 ,这样就有
,这样就有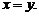 把
把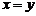 代入③,得
代入③,得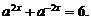
令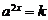 ,则有
,则有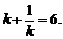 即
即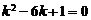 ,∴
,∴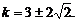
∴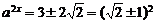 .故
.故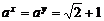 或
或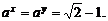
[点评]本题巧妙地求出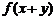 与
与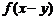 ,再运用方程的思想求解,这种方法在幂的运算中常用到。
,再运用方程的思想求解,这种方法在幂的运算中常用到。
2.分数指数幂的运算性质
(1)有理数幂的运算性质
有理数幂的运算性质形式上与整数指数幂的运算性质完全一样:
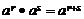 ;
;
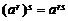 ;
;
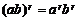 。
。
式中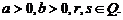
对于这三条性质,不要求证明,但须记准、记熟、会用、用活。
1.幂指数的扩充
|
幂指数 |
定义 |
底数的取值范围 |
|
|
正整数 指数 |
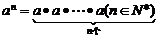 |
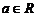 |
|
|
零指数 指数 |
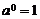 |
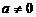 且 且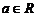 |
|
|
负整数 指数 |
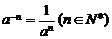 |
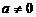 且 且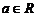 |
|
|
正分数 指数 |
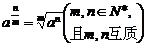 |
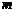 为奇数 为奇数 |
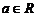 |
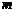 为偶数 为偶数 |
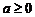 |
||
|
负分数 指数 |
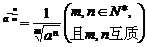 |
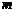 为奇数 为奇数 |
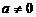 且 且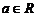 |
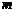 为偶数 为偶数 |
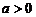 |
||
|
无理数 |
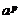 是一个确定的实数 是一个确定的实数(其中 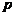 为无理数) 为无理数) |
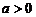 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com