
题目列表(包括答案和解析)
1.关于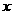 的方程
的方程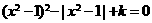 ,给出下列四个命题;
,给出下列四个命题;
①存在实数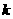 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数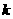 ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数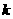 ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数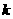 ,使得方程恰有8个不同的实根。
,使得方程恰有8个不同的实根。
其中假命题的个数是( )
A.0 B.1 C.2 D.3
[解析]考查一元二次方程根的分布情况以及绝对值的意义,首先将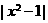 换元成
换元成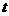 ,原方程变成了
,原方程变成了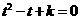 存在两个不等的小于1的正实数根,原方程就存在8个实数根;
存在两个不等的小于1的正实数根,原方程就存在8个实数根;
(2)当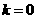 时,使得原方程存在
时,使得原方程存在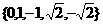 共5个实数根;
共5个实数根;
(3)当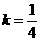 时,使得原方程存在
时,使得原方程存在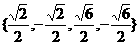 共4个实数根;
共4个实数根;
(4)当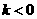 时,方程
时,方程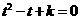 的根为一正一负,故原方程只有2个实数根。
的根为一正一负,故原方程只有2个实数根。
(5)当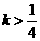 时,原方程无实根,故选A。
时,原方程无实根,故选A。
11.关于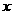 的方程
的方程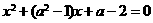 的两根
的两根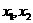 满足
满足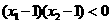 ,则
,则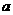 的取值范围为 。
的取值范围为 。
10.根据下表,能够判断方程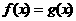 有实数解的区间是
有实数解的区间是
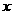 |
-1 |
0 |
1 |
2 |
3 |
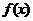 |
-0.677 |
3.011 |
5.432 |
5.980 |
7.651 |
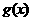 |
-0.530 |
3.451 |
4.890 |
5.241 |
6.892 |
9.二次函数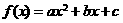 的图象开口向下,对称轴为
的图象开口向下,对称轴为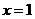 ,在图象与
,在图象与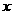 轴的两个交点中,一个交点的横坐标
轴的两个交点中,一个交点的横坐标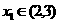 ,则有( )
,则有( )
A.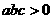 B.
B.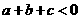 C.
C.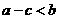 D.
D.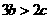
8.已知方程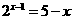 ,则该方程的解会落在区间( )内。
,则该方程的解会落在区间( )内。
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
7.函数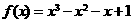 在
在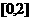 上( )
上( )
A.有三个零点 B.有两个零点 C.有一个零点 D.没有零点
6.若函数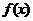 的图象是连续不间断的,且
的图象是连续不间断的,且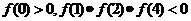 ,则下列命题正确的是( )
,则下列命题正确的是( )
A.函数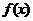 在区间
在区间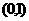 内有零点 B.函数
内有零点 B.函数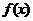 在区间
在区间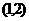 内有零点
内有零点
C.函数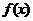 在区间
在区间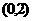 内有零点 D.函数
内有零点 D.函数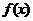 在区间
在区间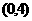 内有零点
内有零点
5.下面关于二分法的叙述正确的是( )
A.用二分法可求函数的所有零点近似解
B.用二分法求方程近似解时,可以精确到小数点后任一位数字
C.二分法根本无规律可循,无法在计算机上进行
D.只在求函数的零点时,才用二分法
4.下列方程在区间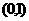 内存在实数解的是( )
内存在实数解的是( )
A.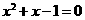 B.
B.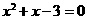
C.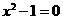 D.
D.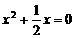
3.已知函数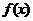 的图象是连续不间断的,有如下的
的图象是连续不间断的,有如下的 对应值表( )
对应值表( )
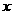 |
1 |
2 |
3 |
4 |
5 |
6 |
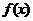 |
123.56 |
21.45 |
-7.82 |
11.57 |
53.76 |
-126.49 |
函数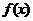 在区间
在区间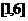 上的零点至少有( )
上的零点至少有( )
A.2个 B.3个 C.4个 D.5个
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com