
题目列表(包括答案和解析)
(4)让学生描述上述计算过程。
(5)用秦九韶算法求多项式的值,与多项式组成有直接关系吗?用秦九韶算法计算上述多项式的值,需要多少次乘法运算和多少次加法运算?
(6)秦九韶算法适用于一般的多项式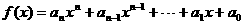 的求值问题吗?
的求值问题吗?
(7)T引导S思考:把n次多项式的求值问题转化成求n个一次多项式的值的问题,即求:
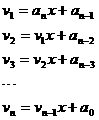
的值的过程,共做了多少次乘法运算,多少次加法运算?
(8)怎样用程序框图表示秦九韶算法?观察秦九韶算法的数学模型,计算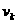 时要用到
时要用到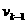 的值,若令
的值,若令
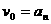 ,我们可以得到下面的递推公式:
,我们可以得到下面的递推公式:

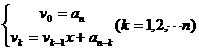
这是一个在秦九韶算法中反复执行的步骤,可以用循环结构来实现。
请画出程序框图。
(9)小结:通过对秦九韶算法的学习,你对算法本身有哪些进一步认识?
(1)设计求多项式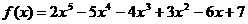 当x=5时的值的算法,并写出程序。
当x=5时的值的算法,并写出程序。
(2)有没有更高效的算法?能否探求更好的算法,来解决任意多项式的求解问题?
T引导学生把多项式变形为:
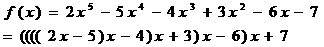
并提问:从内到外,如果把每一个括号都看成一个常数,那么变形后的式子中有哪些“一次式”?x的系数依次是什么?
(3)若将x的值代入变形后的式子中,那么求值的计算过程是怎样的?
|
原多项式x的系数 |
2 |
-5 |
-4 |
3 |
-6 |
7 |
运算 |
|
|
|
|
|
|
|
|
+ |
|
变形后x的“系数” |
|
|
|
|
|
|
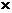 5 5 |
最后得系数2677即为所求的值。
在数学的发展史上,从公元前2、3世纪公元14世纪,中国的数学虽有过高潮,也有过低落,但一直走在世界的前列,是世界数学的中心。中国古代数学对世界数学发展有着不可磨灭的贡献。秦九韶算法就是中国古代数学的一枝奇葩。今天这节课我们领略秦九韶算法的魅力。
7.(2003年上海春季高考题)已知函数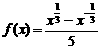 ;
;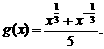
(1)证明 满足
满足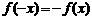 ,并求
,并求 的单调区间;
的单调区间;
(2)分别计算 和
和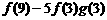 的值,由此概括出涉及函数
的值,由此概括出涉及函数 和
和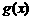 对所有不等于零的实数
对所有不等于零的实数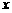 都成立的一个等式,并加以证明。
都成立的一个等式,并加以证明。
[解析](1)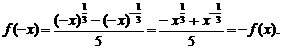
设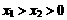 ,由于
,由于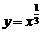 在R上递增,∴
在R上递增,∴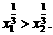
又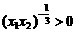 ,
,
∴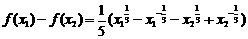
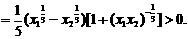
即 在
在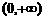 上递增。
上递增。
同理 在
在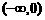 和
和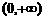 上单调递增。
上单调递增。
(2)∵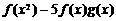
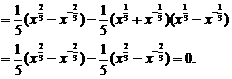
∴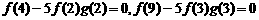 ,
,
且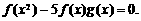
6.(2002年上海文)已知函数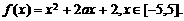
(1)当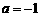 时,求函数
时,求函数 的最大值和最小值;
的最大值和最小值;
(2)求实数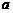 的取值范围,使
的取值范围,使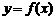 在
在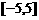 上是单调函数。
上是单调函数。
[解析]当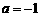 时,
时, 为具体函数,从而求出函数的最值。利用对称轴与区间
为具体函数,从而求出函数的最值。利用对称轴与区间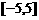 的关系去解(2)的
的关系去解(2)的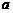 的范围。
的范围。
(1)当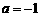 时,
时,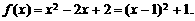
∵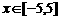 ,
,
故当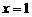 时,
时, 的最小值为1。
的最小值为1。
当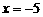 时,
时, 的最大值为37。
的最大值为37。
(2)函数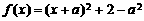 图象的对称轴为
图象的对称轴为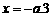
∵ 在
在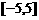 上是单调的,故
上是单调的,故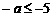 或
或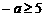 .
.
故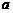 的取值范围是
的取值范围是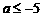 或
或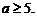
5.(2004年上海理、文)若函数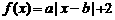 在
在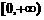 上为增函数,则实数
上为增函数,则实数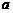 、
、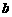 的取值范围是 。
的取值范围是 。
[解析]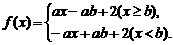
∵函数 在
在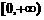 上为增函数,
上为增函数,
∴必有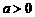 ,且
,且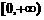 是
是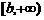 的子集,即
的子集,即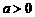 ,且
,且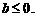
4、(2004年江苏)设函数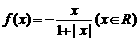 ,区间
,区间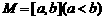 ,集合
,集合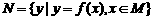 ,则使
,则使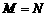 成立的实数对
成立的实数对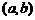 有( )
有( )
A.0个 B.1个 C.2个 D.无数多个
[解析]∵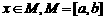 ,则
,则 的定义域为
的定义域为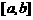 ,
,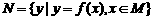 ,∴
,∴ 的值域为
的值域为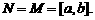 又∵
又∵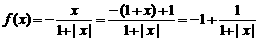 是减函数。∴
是减函数。∴ 在
在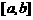 上是减函数,则
上是减函数,则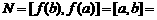 M即
M即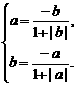 解之
解之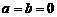 ,这与
,这与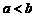 矛盾。
矛盾。
∴实数对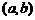 不存在。.
不存在。.
3.(2004年湖南文)若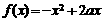 与
与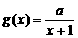 在区间
在区间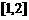 上都是减函数,则
上都是减函数,则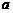 的取值范围是( )
的取值范围是( )
A.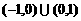 B.
B.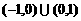 C.
C.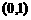 D.
D.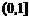
[解析]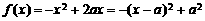 在
在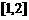 上是减函数的条件是
上是减函数的条件是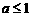 ,又
,又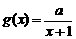 在区间
在区间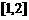 上是减函数的条件是
上是减函数的条件是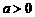 ,故
,故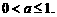 故选D.
故选D.
2.(2003年北京春季高考题)函数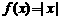 和
和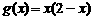 的递增区间依次是( )
的递增区间依次是( )
A.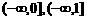 B.
B.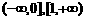
C.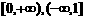 D.
D.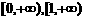
[解析]由图象可知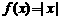 的递增区间为
的递增区间为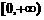 ,而
,而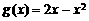 的递增区间为
的递增区间为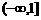 。故选C
。故选C
1.(2003年北京春季高考题)函数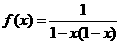 的最大值是( )
的最大值是( )
A.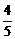 B.
B.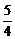 C.
C.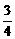 D.
D.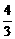
[解析]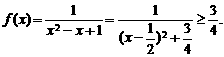 选D。
选D。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com