
题目列表(包括答案和解析)
6.比较大小
比较大小问题一般是利用函数的单调性,当不便利用单调性时,可与0和1去比较,这种方法叫“搭桥”法。
5.幂函数的单调性和奇偶性
幂函数的单调性与奇偶性与一般函数的单调性和奇偶性相同,在证明或判断时,主要应用定义法判断,有时也用幂函数的性质加以判断。
4.求幂函数的定义域、值域
幂函数的定义域要根据解析式来确定,要保证解析式有意义,值域要在定义域范围内求解。
3.幂函数的性质
从上图可以观察到幂函数的特征如下:
 |
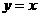 |
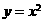 |
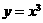 |
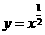 |
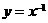 |
|
定义域 |
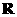 |
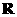 |
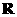 |
 |
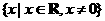 |
|
值域 |
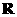 |
 |
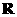 |
 |
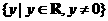 |
|
奇偶性 |
奇 |
偶 |
奇 |
非奇非偶 |
奇 |
|
单调性 |
增 |
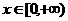 时,增 时,增 |
增 |
增 |
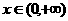 时,减 时,减 |
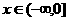 时,减 时,减 |
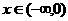 时,减 时,减 |
||||
|
定点 |
(1,1) (0,0) |
(1,1) (0,0) |
(1,1) (0,0) |
(1,1) (0,0) |
(1,1) |
结合以上特征得幂函数的性质如下:
(1)所有的幂函数在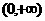 都有定义,并且图象都通过点(1,1);
都有定义,并且图象都通过点(1,1);
(2)如果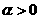 ,则幂函数的图象过原点,并且在区间
,则幂函数的图象过原点,并且在区间 上为增函数;
上为增函数;
(3)如果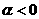 ,则幂函数的图象在区间
,则幂函数的图象在区间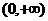 上是减函数,在第一象限内,当
上是减函数,在第一象限内,当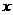 从右边趋向于原点时,图象在
从右边趋向于原点时,图象在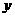 轴右方无限地逼近
轴右方无限地逼近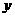 轴,当
轴,当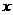 趋向于
趋向于 时,图象在
时,图象在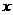 轴上方无限地逼近
轴上方无限地逼近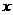 轴;
轴;
(4)当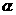 为奇数时,幂函数为奇函数,当
为奇数时,幂函数为奇函数,当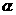 为偶函数,幂函数为偶函数。
为偶函数,幂函数为偶函数。
2.幂函数的图象
我们只讨论幂函数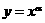 中
中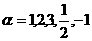 时的图象。
时的图象。
在同一平面直角坐标系作出幂函数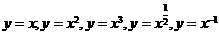 的图象。
的图象。
(1)列表、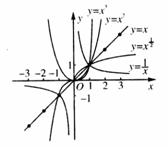 (2)描点:3)连线:用光滑的曲线将各点连结起来。如图
(2)描点:3)连线:用光滑的曲线将各点连结起来。如图
(2)记熟上面各函数图象的形状,及它们之间的“高低”关系。(3)函数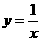 可记为
可记为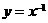 。(4)
。(4)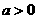 时,图象都过
时,图象都过 点,
点,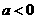 时,只过(1,1)不过(0,0)点。
时,只过(1,1)不过(0,0)点。
1.幂函数的概念
(1)一般地,幂函数的表达式为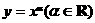 ,其中
,其中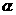 为常数;其特征是以幂的底为自变量,指数为常数。
为常数;其特征是以幂的底为自变量,指数为常数。
(2)所有的幂函数在区间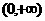 都有定义,并且图象都通过点(1,1)。
都有定义,并且图象都通过点(1,1)。
(3)学习和理解幂函数的概念时要注意以下几点:
①形如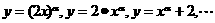 形式的函数不是幂函数。
形式的函数不是幂函数。
②幂函数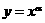 中的
中的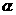 为任意实数。
为任意实数。
③确定一个幂函数,只需求出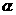 即可。
即可。
12、已知函数f(x) = x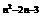 (n∈Z)的图象与两坐标轴都无公共点,且其图象关于 y轴对称,求n的值并画出相应的函数图象.
(n∈Z)的图象与两坐标轴都无公共点,且其图象关于 y轴对称,求n的值并画出相应的函数图象.
11、比较下列各组中两个数的大小:
(1)2.5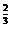 ,(-1.4)
,(-1.4)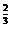 ,(-3)
,(-3)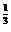 ; (2)4.1
; (2)4.1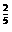 ,3.8
,3.8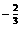 ,(-1.9)
,(-1.9) ;
;
(3)0.16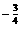 ,0.5
,0.5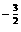 ,6.25
,6.25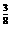 .
.
10、对于函数y = x2,y = x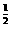 有下列说法:①两个函数都是幂函数;②两个函数在第一象限内都单调递增;③它们的图象关于直线y = x对称;④两个函数都是偶函数;⑤两个函数都经过点(0,0),(1,1);⑥两个函数互为反函数。其中正确的说法是_______________.
有下列说法:①两个函数都是幂函数;②两个函数在第一象限内都单调递增;③它们的图象关于直线y = x对称;④两个函数都是偶函数;⑤两个函数都经过点(0,0),(1,1);⑥两个函数互为反函数。其中正确的说法是_______________.
9、在函数①y = x3,②y = x 2,③y = x -1,④y = 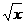 中,定义域和对应的值域相同的有______________________.
中,定义域和对应的值域相同的有______________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com