
题目列表(包括答案和解析)
(三)幂函数
1、幂函数定义:一般地,形如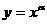
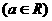 的函数称为幂函数,其中
的函数称为幂函数,其中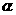 为常数.
为常数.
2、幂函数性质归纳.
(1)所有的幂函数在(0,+∞)都有定义并且图象都过点(1,1);
(2)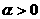 时,幂函数的图象通过原点,并且在区间
时,幂函数的图象通过原点,并且在区间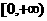 上是增函数.特别地,当
上是增函数.特别地,当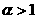 时,幂函数的图象下凸;当
时,幂函数的图象下凸;当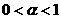 时,幂函数的图象上凸;
时,幂函数的图象上凸;
(3)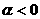 时,幂函数的图象在区间
时,幂函数的图象在区间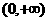 上是减函数.在第一象限内,当
上是减函数.在第一象限内,当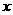 从右边趋向原点时,图象在
从右边趋向原点时,图象在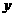 轴右方无限地逼近
轴右方无限地逼近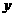 轴正半轴,当
轴正半轴,当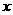 趋于
趋于 时,图象在
时,图象在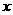 轴上方无限地逼近
轴上方无限地逼近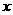 轴正半轴.
轴正半轴.
例题:
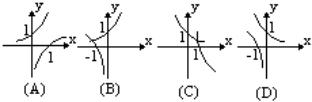
1. 已知a>0,a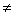 0,函数y=ax与y=loga(-x)的图象只能是 ( )
0,函数y=ax与y=loga(-x)的图象只能是 ( )
2.计算: ①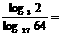 ;②
;② = ;
= ;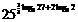 =
;
=
;
③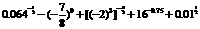 =
=
3.函数y=log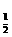 (2x2-3x+1)的递减区间为
(2x2-3x+1)的递减区间为
4.若函数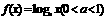 在区间
在区间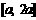 上的最大值是最小值的3倍,则a=
上的最大值是最小值的3倍,则a=
5.已知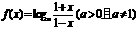 ,(1)求
,(1)求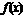 的定义域(2)求使
的定义域(2)求使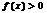 的
的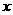 的取值范围
的取值范围
第三章 函数的应用
(二)对数函数
1、对数函数的概念:函数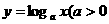 ,且
,且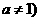 叫做对数函数,其中
叫做对数函数,其中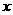 是自变量,函数的定义域是(0,+∞).
是自变量,函数的定义域是(0,+∞).
注意:1 对数函数的定义与指数函数类似,都是形式定义,注意辨别。如: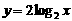 ,
, 都不是对数函数,而只能称其为对数型函数.
都不是对数函数,而只能称其为对数型函数.
2 对数函数对底数的限制: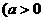 ,且
,且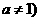 .
.
2、对数函数的性质:
|
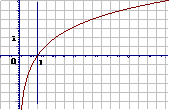
a>1 |
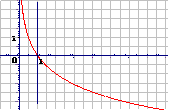
0<a<1 |
|
 |
 |
|
|
定义域x>0 |
定义域x>0 |
|
|
值域为R |
值域为R |
|
|
在R上递增 |
在R上递减 |
|
|
函数图象都过定点(1,0) |
函数图象都过定点(1,0) |
(二)对数的运算性质
如果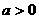 ,且
,且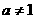 ,
,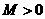 ,
,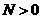 ,那么:
,那么:
1 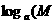 ·
·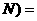
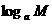 +
+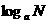 ;
;
2 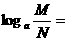
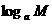 -
-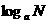 ;
;
3 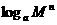
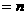
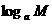
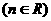 .
.
注意:换底公式
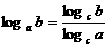 (
(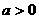 ,且
,且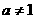 ;
;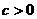 ,且
,且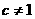 ;
;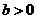 ).
).
利用换底公式推导下面的结论
(1)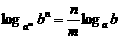 ;(2)
;(2)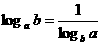 .
.
(一)对数
1.对数的概念:一般地,如果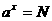
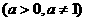 ,那么数
,那么数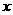 叫做以
叫做以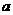 为底
为底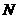 的对数,记作:
的对数,记作: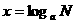 (
(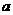 - 底数,
- 底数,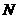 - 真数,
- 真数,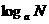 - 对数式)
- 对数式)
说明:1 注意底数的限制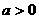 ,且
,且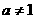 ;
;
 2
2 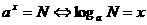 ;
;
3 注意对数的书写格式.
两个重要对数:
1 常用对数:以10为底的对数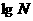 ;
;
2 自然对数:以无理数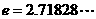 为底的对数的对数
为底的对数的对数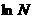 .
.
u 指数式与对数式的互化
幂值 真数





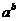 = N
= N
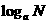 = b
= b

底数
 指数
对数
指数
对数
(二)指数函数及其性质
1、指数函数的概念:一般地,函数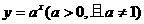 叫做指数函数,其中x是自变量,函数的定义域为R.
叫做指数函数,其中x是自变量,函数的定义域为R.
注意:指数函数的底数的取值范围,底数不能是负数、零和1.
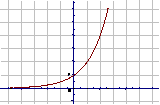
2、指数函数的图象和性质
|
a>1 |
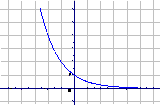
0<a<1 |
 |
 |
|
定义域 R |
定义域 R |
|
值域y>0 |
值域y>0 |
|
在R上单调递增 |
在R上单调递减 |
|
非奇非偶函数 |
非奇非偶函数 |
|
函数图象都过定点(0,1) |
函数图象都过定点(0,1) |
注意:利用函数的单调性,结合图象还可以看出:
(1)在[a,b]上,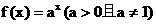 值域是
值域是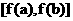 或
或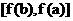 ;
(2)若
;
(2)若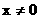 ,则
,则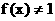 ;
;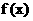 取遍所有正数当且仅当
取遍所有正数当且仅当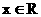 ;
(3)对于指数函数
;
(3)对于指数函数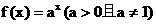 ,总有
,总有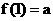 ;
;
(一)指数与指数幂的运算
1.根式的概念:一般地,如果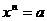 ,那么
,那么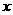 叫做
叫做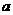 的
的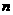 次方根,其中
次方根,其中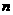 >1,且
>1,且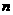 ∈
∈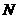 *.
*.
u
负数没有偶次方根;0的任何次方根都是0,记作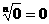 。
。
当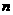 是奇数时,
是奇数时,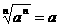 ,当
,当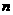 是偶数时,
是偶数时,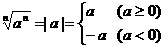
2.分数指数幂
正数的分数指数幂的意义,规定:
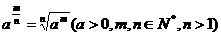 ,
,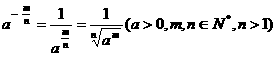
u 0的正分数指数幂等于0,0的负分数指数幂没有意义
3.实数指数幂的运算性质
(1)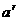 ·
·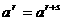
 ;
;
(2)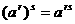
 ;
;
(3)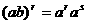
 .
.
11.设函数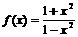 判断它的奇偶性并且求证:
判断它的奇偶性并且求证: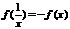 .
.
第二章 基本初等函数
10.判断函数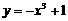 的单调性并证明你的结论.
的单调性并证明你的结论.
9.求下列函数的单调区间:
⑴ 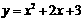 ⑵
⑵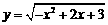 ⑶
⑶ 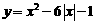
8.设 是R上的奇函数,且当
是R上的奇函数,且当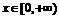 时,
时,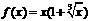 ,则当
,则当 时
时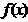 =
=
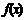 在R上的解析式为
在R上的解析式为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com