
题目列表(包括答案和解析)
1、函数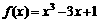 在闭区间[-3,0]上的最大值、最小值分别是 ( C )
在闭区间[-3,0]上的最大值、最小值分别是 ( C )
(A)1,-1 (B)1,-17 (C)3,-17 (D)9,-19 (2004江苏)
32.在如图所示的电路中,开关b,a,c开或关的概率都为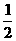 ,且相互独立,求灯亮的概率.
,且相互独立,求灯亮的概率.
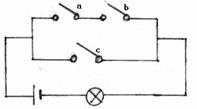
解法1:设事件A、B、C分别表示开关a,b,c关闭,则a,b同时关合或c关合时灯亮,即A·B·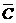 ,A·B·C或
,A·B·C或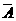 ·B·C,A·
·B·C,A·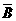 ·C,
·C,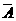 ·
·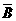 ·C之一发生,又因为它们是互斥的,所以,所求概率为
·C之一发生,又因为它们是互斥的,所以,所求概率为
P=P(A·B·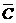 )+P(
)+P(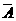 ·B·C)+P(A·
·B·C)+P(A·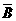 ·C)+P(
·C)+P(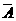 ·
·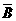 ·C)+P(A·B·C)
·C)+P(A·B·C)
=P(A)·P(B)·P(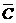 )+P(
)+P(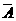 )·P(B)·P(C)+P(A)·P(
)·P(B)·P(C)+P(A)·P(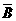 )·P(C)
)·P(C)
+P(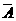 )·P(
)·P(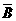 )·P(C)+P(A)·P(B)·P(C)=
)·P(C)+P(A)·P(B)·P(C)=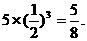
解法2:设A,B,C所表示的事件与解法1相同,若灯不亮,则两条线路都不通,即C一定开,a,b中至少有一个开.而a,b中至少有一个开的概率是
1-P(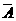 ·
·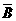 )=1-P(
)=1-P(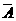 )·P(
)·P(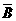 )=
)=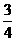 ,
,
所以两条线路皆不通的概率为
P(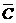 )·[1-P(
)·[1-P(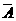 ·
·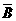 )]=
)]=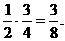
于是,灯亮的概率为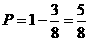 .答:略.
.答:略.
31.某人忘记了电话号码的最后一个数字,因而他随意地拨号,假设拨过了的号码不再重复,试求下列事件的概率:
(1)第3次拨号才接通电话;
(2)拨号不超过3次而接通电话.
解:设A1={第i次拨号接通电话},i=1,2,3.
(1)第3次才接通电话可表示为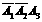 于是所求概率为
于是所求概率为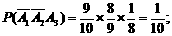
(2)拨号不超过3次而接通电话可表示为:A1+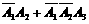 于是所求概率为
于是所求概率为
P(A1+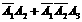 )=P(A1)+P(
)=P(A1)+P(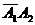 )+P(
)+P(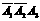 )=
)=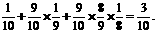
30、在120个零件中.一级品24个,二级品36个,三级品60个,从中抽取容量为20的样本。
(1) 分别用简单随机抽样和分层抽样计算每个个体被抽到的概率。
(2) 用上述哪一种抽样使一级品中某甲与二级品中某乙都被抽到的概率较大。
[解] (1)用简单随机抽样,每个个体被抽到的概率为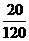 =
=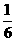
用分层抽样:一、二、三级品被抽取数分别为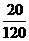 ×24=4,
×24=4,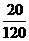 ×36=6,
×36=6,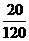 ×60=10。
×60=10。
故每层中每个个体被抽到的概率分别为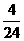 ,
, ,
,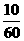 即都是
即都是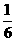 。
。
(2)用分层抽样时,因为在一级品抽样与在二级品中抽样是独立的,故一级品甲与二级 品乙都被抽到的概率为P=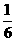 ·
·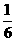 =
=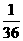 。
。
用简单随机抽样时一级品甲与二级品乙都被抽到的概率为
P′=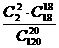 =
=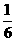 ×
×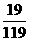 <
<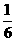 ×
×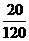 =
=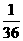 。
。
故用分层抽样时,一级品甲与二级品乙都被抽到的概率较大.
29、某班50名学生,现在采用随机抽样方法逐一从中抽取5名同学参加夏令营,学生甲最后一个去抽,则他被拍中的概率为
(A)0.1 (B)0.02 (C)0或1 (D)以上都不对
[分析] 因为用简单随机抽样从个体数为50的总体中抽取一个容量为5的样本,那么 每个个体被抽到的概率都等于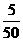 =
=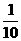 ,不论学生甲抽取的位置,他抽到参加夏令营的资格均为
,不论学生甲抽取的位置,他抽到参加夏令营的资格均为 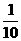 =0.1.故选A.
=0.1.故选A.
28、用分层抽样法从10名男生5名女生中抽取3人参加智力游戏.试求某一男生甲以及某-女生乙分别被抽到的概率。
解∵抽样比为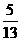 ∴抽取男生
∴抽取男生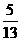 ×10=2人 抽取女生
×10=2人 抽取女生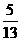 × 5=l人
× 5=l人
∴某男生甲被抽到的概率为P1=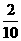 =
=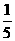
某女生乙被抽到的概率为P2=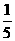
27.某厂生产的A产品按每盒10件进行包装,每盒产品均需检验合格后方可出厂.质检办法规定:从每盒10件A产品中任抽4件进行检验,若次品数不超过1件,就认为该盒产品合格;否则,就认为该盒产品不合格.已知某盒A产品中有2件次品.
(1)求该盒产品被检验合格的概率;
(2)若对该盒产品分别进行两次检验,求两次检验得出的结果不一致的概率.
解: (1) 被检验认为是合格的概率为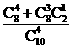 …
…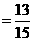
(2)两次检验是相互独立的,可视为独立重复试验,
故“两次检验得出的结果不一致”即两次检验中恰有一次是合格的概率为
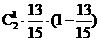
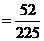 .
.
0.1512 0.3924。
26.甲、乙两个篮球运动员,投篮的命中率分别为0.6和0.8。如果每人投篮两次。
(1)求甲投进2球,且乙投进1球的概率;
(2)若投进1个球得2分,未投进得0分,求甲、乙两人得分相等的概率。
25.高二(8)班有6名同学是1988年9月份生的,求至少有2人是同一天生的概率。
解:记事件 =“6人中至少有两人同一天出生”,
=“6人中至少有两人同一天出生”, 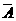 =“6人中没有2人的生日相同”。九月份共30天,每个人可以是30天中任一天出生,全部可能的情况为
=“6人中没有2人的生日相同”。九月份共30天,每个人可以是30天中任一天出生,全部可能的情况为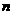 =
=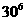 ,没有二人生日相同,就是30天中取6个的排列数
,没有二人生日相同,就是30天中取6个的排列数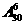 ,得
,得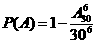 ≈0.4136。
≈0.4136。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com