
题目列表(包括答案和解析)
3.
顶点在原点,以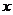 轴为对称轴且经过点
轴为对称轴且经过点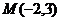 的抛物线的标准方程为____________.
的抛物线的标准方程为____________.
2.
在二项式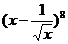 的展开式中,含
的展开式中,含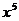 的项的系数是 (用数字作答).
的项的系数是 (用数字作答).
1.
如果复数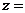
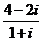 (其中
(其中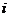 为虚数单位),那么
为虚数单位),那么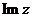 (即
(即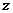 的虚部)为__________。
的虚部)为__________。
21.已知函数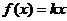 ,
,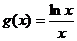
(1)求函数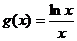 的单调递增区间;
的单调递增区间;
(2)若不等式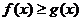 在区间(0,+
在区间(0,+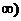 上恒成立,求
上恒成立,求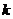 的取值范围;
的取值范围;
(3)求证: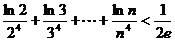
解:(1)∵ 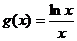 (
(
∴ 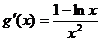 令
令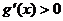 ,得
,得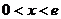
故函数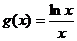 的单调递增区间为
的单调递增区间为 ………………………………………………3分
………………………………………………3分
(2)由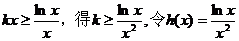
则问题转化为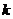 大于等于
大于等于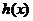 的最大值 …………………………………………5分
的最大值 …………………………………………5分
又 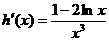 …………………………………………………………………………6分
…………………………………………………………………………6分
令 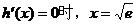
当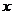 在区间(0,+
在区间(0,+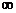 )内变化时,
)内变化时,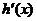 、
、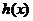 变化情况如下表:
变化情况如下表:
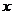 |
(0, ) ) |
 |
( ,+ ,+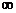 ) ) |
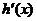 |
+ |
0 |
- |
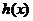 |
↗ |
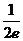 |
↘ |
由表知当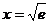 时,函数
时,函数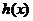 有最大值,且最大值为
有最大值,且最大值为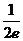 ……………………………..8分
……………………………..8分
因此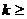
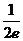 ………………………………………………………………………………….9分
………………………………………………………………………………….9分
(3)由(2)知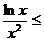
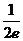 ,
,
∴ 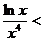
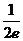
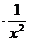 (
(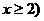 ……………………………………………………………….10分
……………………………………………………………….10分
∴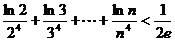 (
(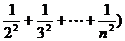 ……………………………………12分
……………………………………12分
又∵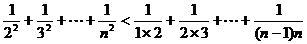
=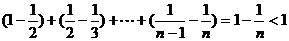
∴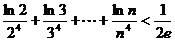 ……………………………………………………………14分
……………………………………………………………14分
20.已知数列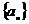 的通项公式为
的通项公式为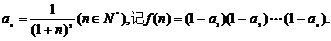
(1)试求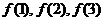 的值;
的值;
(2)猜想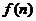 的值,并用数学归纳法证明你的猜
的值,并用数学归纳法证明你的猜
解:(1)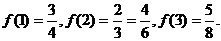
(2)猜想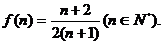

19.由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:


(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅲ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记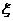 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求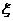 的分布列及数学期望.
的分布列及数学期望.
解:(Ⅰ)众数:4.6和4.7;中位数:4.75
(Ⅱ)设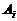 表示所取3人中有
表示所取3人中有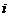 个人是“好视力”,至多有1人是“好视力”记为事件
个人是“好视力”,至多有1人是“好视力”记为事件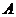 ,则
,则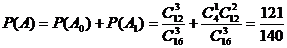
(Ⅲ)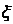 的可能取值为0、1、2、3
的可能取值为0、1、2、3
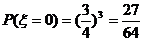 ;
; 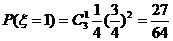
 ;
;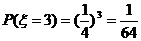
分布列为
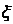
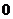
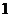
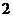
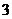
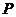
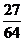
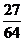
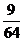
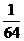
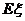
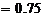 .
.
另解: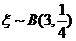 ,
,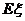 =
=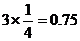
18.已知函数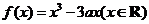 .
.
(Ⅰ)当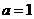 时,求
时,求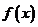 的极小值;
的极小值;
(Ⅱ)若直线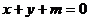 对任意的
对任意的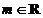 都不是曲线
都不是曲线 的切线,求
的切线,求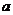 的取值范围.
的取值范围.
解:(Ⅰ)因为当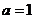 时,
时,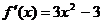 ,令
,令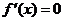 ,得
,得 或
或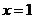 .
.
当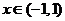 时,
时,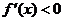 ;当
;当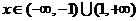 时,
时,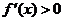 .
.
所以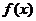 在
在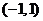 上单调递减,在
上单调递减,在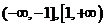 上单调递增.
上单调递增.
所以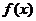 的极小值为
的极小值为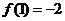 .
.
(Ⅱ)因为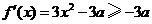 ,
,
所以,要使直线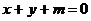 对任意的
对任意的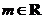 总不是曲线
总不是曲线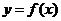 的切线,当且仅当
的切线,当且仅当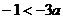 ,即
,即 .
.
17.如图,节日花坛中有5个区域,现有n种不同颜色的花
 装饰这5个区域中(不必每种颜色的花都用),
装饰这5个区域中(不必每种颜色的花都用),
要求相同颜色的花不能相邻,求:
(1)n=3时,一共有多少种装饰方案?
(2)n=4时,花坛只用3种颜色的花装饰的概率
16.
已知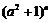 的展开式中各项系数之和等于
的展开式中各项系数之和等于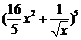 的展开式的常数项,并且
的展开式的常数项,并且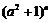 的展开式中系数最大的项等于54,求
的展开式中系数最大的项等于54,求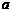 的值.
的值.
解: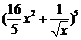 展开式的常数项为:
展开式的常数项为: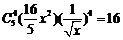 3分
3分
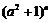 展开式的系数之和
展开式的系数之和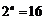 ,n = 4 6分
,n = 4 6分
∴ 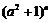 展开式的系数最大的项为
展开式的系数最大的项为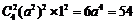 , 10分
, 10分
∴ 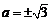 12分
12分
15. 下列2题中任选一题做
(1)在直角坐标系中圆C的参数方程为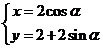 (
(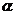 为参数),若以原点
为参数),若以原点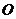 为极点,以
为极点,以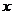 轴正半轴为极轴建立极坐标系,则圆
轴正半轴为极轴建立极坐标系,则圆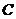 的极坐标方程为___ __.
的极坐标方程为___ __.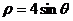
(2)不等式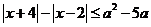 对任意实数x恒成立,则实数a的取值范围是
对任意实数x恒成立,则实数a的取值范围是
(-∞,-1]∪[6,+∞)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com