
题目列表(包括答案和解析)
5.设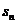 为等比数列
为等比数列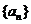 的前n项和,
的前n项和,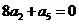 则
则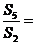
(A)-11 (B)-8 (C)5 (D)11
解析:通过 ,设公比 为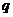 ,将该式转化为
,将该式转化为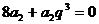 ,解得
,解得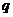 =-2,带入所求式可知答案选A,本题主要考察了本题主要考察了等比数列的通项公式与前n项和公式
=-2,带入所求式可知答案选A,本题主要考察了本题主要考察了等比数列的通项公式与前n项和公式
4.某程序框图所示,若输出的S=57,则判断框内为
(A) k>4? (B) k>5? (C) k>6? (D) k>7?
解析:选A,本题主要考察了程序框图的结构,以及与数列有关的简单运算,属容易题
3.设i为虚数单位,则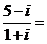
(A)-2-3i (B)-2+3i (C)2-3i (D)2+3i
解析:选C,本题主要考察了复数代数形式的四则运算,属容易题
2. 已知函数
已知函数 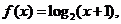 若
若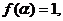
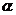 =
=
(A)0 (B)1 (C)2 (D)3
解析: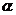 +1=2,故
+1=2,故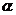 =1,选B,本题主要考察了对数函数概念及其运算性质,属容易题
=1,选B,本题主要考察了对数函数概念及其运算性质,属容易题
1.设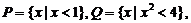 则
则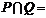
(A)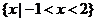 (B)
(B)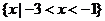 (C)
(C)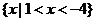 (D)
(D)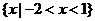
解析: ,故答案选D,本题主要考察了集合的基本运算,属容易题
20.(15分)已知m是非零实数,抛物线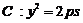 (p>0)
(p>0)
的焦点F在直线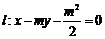 上。(I)若m=2,求抛物线C的方程
上。(I)若m=2,求抛物线C的方程
(II)设直线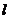 与抛物线C交于A、B,△A
与抛物线C交于A、B,△A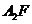 ,△
,△ 的重心分别为G,H
的重心分别为G,H
 求证:对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外。
求证:对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外。
19..(14分)已知函数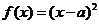 (a-b)
(a-b)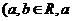 <b)。
<b)。
(I)当a=1,b=2时,求曲线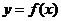 在点(2,
在点(2,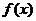 )处的切线方程。
)处的切线方程。
(II)设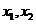 是
是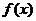 的两个极值点,
的两个极值点,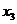 是
是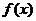 的一个零点,且
的一个零点,且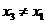 ,
,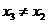
证明:存在实数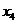 ,使得
,使得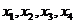 按某种顺序排列后的等差数列,并求
按某种顺序排列后的等差数列,并求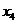 .
.
18.如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9.电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999. (Ⅰ)求p;
(Ⅱ)求电流能在M与N之间通过的概率。
(Ⅲ)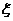 表示T1,T2,T3,T4中能通过电流的元件个数,求
表示T1,T2,T3,T4中能通过电流的元件个数,求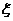 的期望.
的期望.

17.(14分)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°。E为线段AB的中点,将△ADE沿直线DE翻折成△A’DE,使平面A’DE⊥平面BCD,F为线段A’C的中点。
(Ⅰ)求证:BF∥平面A’DE;
(Ⅱ)设M为线段DE的中点,求直线FM与平面A’DE所成角的余弦值。

16.(12分)设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,满足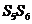 +15=0。 (Ⅰ)若
+15=0。 (Ⅰ)若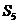 =5,求
=5,求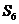 及a1; (Ⅱ)求d的取值范围。
及a1; (Ⅱ)求d的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com