(一)知识教学点

掌握两条直线平行与垂直的条件，会运用条件判断两直线是否平行或垂直，能运用条件确定两平行或垂直直线的方程系数．

4．等腰三角形一腰所在的直线l1的方程是2x-y+4=0，底面所在的直线l2的方程是x+y-1=0，点(-2，0)在另一腰上，求这腰所在的直线l3的方程．

解：这是本课例3将l1与l3互换的变形题，解法与例3相同，所求方程为：

x-2y-2=0．

3．(习题三第10题)已知直线l经过点P(2，1)，且和直线5x+2y+3=0的夹角为45o，求直线l的方程．

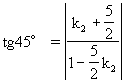
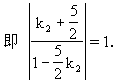
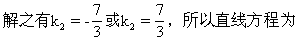
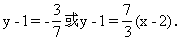
即3x+7y-13=0或7x-3y-11=0．

2．(教材第32页，1．8练习第2题)求下列直线的夹角：

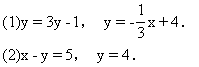
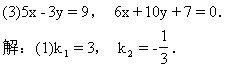
∵k1·k2=-1，

∴l1与l2的夹角是90°．

(2)k1=1，　 k2=0．

两直线的夹角为45°．

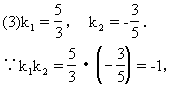
∴l1与l2的夹角是90°．

1．(教材第32页，1．8练习第1题)求下列直线l1到l2的角与l2到l1的角：

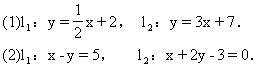
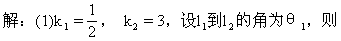
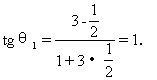
∴θ1=45°．

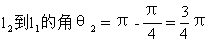
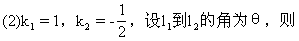
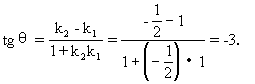
l2到l1的角θ2=π-θ1=arctg3．

(五)课后小结

(1)l1到l2的角的概念及l1与l2夹角的概念；

(2)l1到l2的角的正切公式；

(3)l1与l2的夹角的正切公式；

(4)等腰三角形中，一腰所在直线到底面所在直线的角，等于底边所在直线到另一腰所在直线的角．

(四)例题

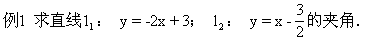
解：k1=-2，k2=1．

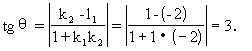
∴θ=arctg3≈71°34′．

本例题用来熟悉夹角公式．

例2　 已知直线l1：　 A1x+B1y+C1=0和l2：　 A2x+B2y+C2=0(B1≠0、B2≠0、A1A2+B1B2≠0)，l1到l2的角是θ，求证：

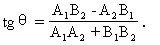
证明：设两条直线l1、l2的斜率分别为k1、k2，则

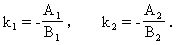
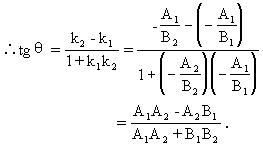
这个例题用来熟悉直线l1到l2的角．

例3等腰三角形一腰所在的直线l1的方程是x-2y-2=0，底边所在的直线l2的方程是x+y-1=0，点(-2，0)在另一腰上，求这腰所在直线l3的方程．

解：先作图演示一腰到底的角与底到另一腰的角相等，并且与两腰到底的角与底到另一腰的角相等，并且与两腰的顺序无关．

设l1、l2、l3的斜率分别是k1、k2、k3，l1到l2的角是θ1，l2到l3的角是θ2，则

．

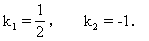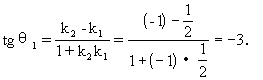
因为l1、l2、l3所围成的三角形是等腰三角形，所以

θ1=θ2．

tgθ2=tgθ1=-3．

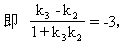
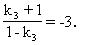
解得　 k3=2．

因为l3经过点(-2，0)，斜率为2，写出点斜式为

y=2[x-(-2)]，

即　 2x-y+4=0．

这就是直线l3的方程．

讲此例题时，一定要说明：无须作图，任一腰到底的角与底到另一腰的角都相等，要为锐角都为锐角，要为钝角都为钝角．

(三)夹角公式

从一条直线到另一条直线的角，可能不大于直角，也可能大于直角，但我们常常只需要考虑不大于直角的角(就是两条直线所成的角，简称夹角)就可以了，这时可以用下面的公式

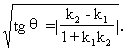
(二)l1到l2的角正切

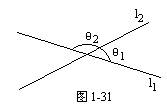
两条直线l1和l2相交构成四个角，它们是两对对顶角．为了区别这些角，我们把直线l1依逆时针方向旋转到与l2重合时所转的角，叫做l1到l2的角．图1-27中，直线l1到l2的角是θ1，l2到l1的角是θ2(θ1+θ2=180°)．

l1到l2的角有三个要点：始边、终边和旋转方向．

现在我们来求斜率分别为k1、k2的两条直线l1到l2的角，设已知直线的方程分别是

l1∶y=k1x+b1　 l2∶y=k2x+b2

如果1+k1k2=0，那么θ=90°，

下面研究1+k1k2≠0的情形．

由于直线的方向是由直线的倾角决定的，所以我们从研究θ与l1和l2的倾角的关系入手考虑问题．

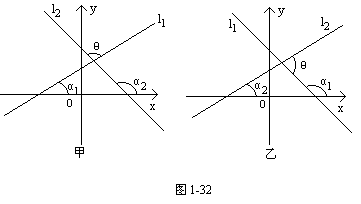
设l1、l2的倾斜角分别是α1和α2(图1-32)，甲图的特征是l1到l2的角是l1、l2和x轴围成的三角形的内角；乙图的特征是l1到l2的角是l1、l2与x轴围成的三角形的外角．

tgα1=k1，　 tgα2=k2．

∵θ=α2-α1(图1-32)，

或θ=π-(α1-α2)=π+(α2-α1)，

∴tgθ=tg(α2-α1)．

或tgθ=tg[π(α2-α1)]=tg(α2-α1)．

可得

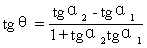
即

eq \x( )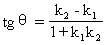

上面的关系记忆时，可抓住分子是终边斜率减始边斜率的特征进行记忆．

(一)引入新课

我们已经研究了直角坐标平面两条直线平行与垂直的情况，对于两条相交直线，怎样根据它们的直线方程求它们所成的角是我们下面要解决的问题．