
题目列表(包括答案和解析)
[例1] (1)已知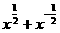 =3,求
=3,求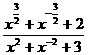 的值;
的值;
(2)已知lg(x+y)+lg(2x+3y)-lg3=lg4+lgx+lgy,求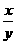 的值.
的值.
(1)分析:由分数指数幂运算性质可求得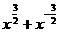 和x2+x-2的值.
和x2+x-2的值.
解:∵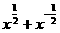 =3,
=3,
∴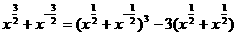
=33-3×3=18.
x2+x-2=(x+x-1)2-2=[(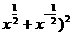 -2]2-2=(32-2)2-2=47.
-2]2-2=(32-2)2-2=47.
∴原式=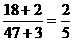 .
.
(2)分析:注意x、y的取值范围,去掉对数符号,找到x、y的关系式.
解:由题意可得x>0,y>0,由对数运算法则得
lg(x+y)(2x+3y)=lg(12xy),
则(x+y)(2x+3y)=12xy.
(2x-y)(x-3y)=0,
即2x=y或x=3y.
故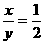 或
或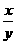 =3.
=3.
评注:条件代数式的求值问题包括以下三个方面:(1)若条件简单,结论复杂,可从化简结论入手用上条件;(2)若条件复杂,结论简单,可从化简条件入手,转化成结论的形式;(3)若条件与结论的复杂程度相差无几时,可同时对它们进行化简,直到找出它们之间的联系为止.
对于齐次方程的化简,也可在方程两边同除以某一齐次项,把方程转化成要求的代数式为未知数的方程的形式.
●知识网络

●范题精讲
19.(本小题满分12分)已知函数f(x)=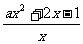 的定义域恰为不等式log2(x+3)+
的定义域恰为不等式log2(x+3)+ 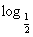 x≤3的解集,且f(x)在定义域内单调递减,求实数a的取值范围.
x≤3的解集,且f(x)在定义域内单调递减,求实数a的取值范围.
解:由log2(x+3)+ 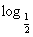 x≤3得
x≤3得
log2(x+3)≤3+log2x=log28x.
∴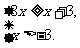 ∴x≥
∴x≥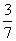 .设x2>x1≥
.设x2>x1≥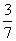 ,
,
f(x2)-f(x1)=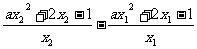
=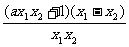 .
.
∵f(x)在[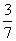 ,+∞)上单调递减,
,+∞)上单调递减,
∴f(x2)<f(x1),即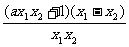 <0.
<0.
∵x1x2>0,x1-x2<0,∴ax1x2+1>0,即a>-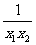 .
.
由x2>x1≥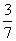 知x1x2>
知x1x2>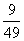 ,∴-
,∴-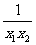 <-
<-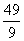 ∴a≥-
∴a≥-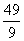 .
.
18.(本小题满分12分)已知二次函数f(x)的二次项系数为负数,且对任意x恒有f(2-x)=f(2+x)成立,解不等式f[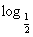 (x2+x+
(x2+x+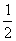 )]>f[
)]>f[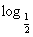 (2x2-x+
(2x2-x+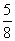 )].
)].
解:因为对任意x,恒有f(2-x)=f(2+x)成立,可得二次函数f(x)的对称轴是x=2.
∵x2+x+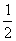 =(x+
=(x+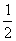 )2+
)2+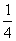 ≥
≥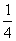 ,
,
2x2-x+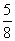 =2(x-
=2(x-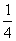 )2+
)2+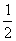 ≥
≥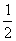 ,
,
∴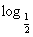 (x2+x+
(x2+x+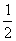 )≤
)≤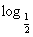
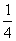 =2,
=2,
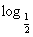 (2x2-x+
(2x2-x+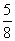 )≤
)≤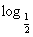 (
(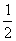 )=1.
)=1.
∵二次函数f(x)的二次项系数为负数,
∴在对称轴左侧f(x)为增函数.
∴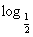 (x2+x+
(x2+x+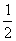 )>
)>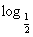 (2x2-x+
(2x2-x+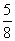 )
)
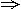 x2+x+
x2+x+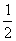 <2x2-x+
<2x2-x+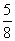
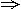 x2-2x+
x2-2x+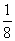 >0
>0
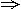 x<-
x<-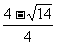 或x>
或x>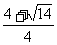 .
.
故不等式的解集为(-∞,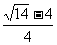 )∪(
)∪(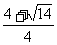 ,+∞).
,+∞).
17.(本小题满分12分)某电器公司生产A型电脑.1993年这种电脑每台平均生产成本为5000元,并以纯利润20%确定出厂价.从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低.到1997年,尽管A型电脑出厂价仅是1993年出厂价的80%,但却实现了50%纯利润的高效益.
(1)求1997年每台A型电脑的生产成本;
(2)以1993年的生产成本为基数,求1993年至1997年生产成本平均每年降低的百分数.(精确到0.01,以下数据可供参考: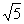 =2.236,
=2.236,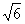 =2.449)
=2.449)
分析:出厂价=单位商品的成本+单位商品的利润.
解:(1)一方面可以根据1993年的出厂价求得1997年的出厂价;另一方面根据题意可把1997年的出厂价用1997年的生产成本表示,列出方程求解.
设1997年每台电脑的生产成本为x元,依题意,得
x(1+50%)=5000×(1+20%)×80%,解得x=3200(元).
(2)因为1993年至1997年四年间成本平均每年降低的百分率相等,因此可把1997年每台的生产成本用这个百分率来表示,而这个量应与第(1)问中求得的1997年每台电脑的生产成本相等,据此列出方程求解.
设1993年至1997年间每年平均生产成本降低的百分率为y,则依题意,得5000(1-y)4=3200,
解得y1=1-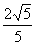 ,y2=1+
,y2=1+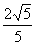 (舍去).
(舍去).
所以,y=1-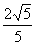 ≈0.11=11%.
≈0.11=11%.
即1997年每台电脑的生产成本为3200元,1993年至1997年生产成本平均每年降低11%.
16.(本小题满分10分)已知y=log4(2x+3-x2).
(1)求定义域;
(2)求f(x)的单调区间;
(3)求y的最大值,并求取最大值时x的值.
解:(1)由2x+3-x2>0,解得-1<x<3.
∴f(x)的定义域为{x|-1<x<3}.
(2)令u=2x+3-x2,则u>0,y=log4u.
由于u=2x+3-x2=-(x-1)2+4.
再考虑定义域可知,其增区间是(-1,1),减区间是[1,3).
又y=log4u在(0,+∞)上为增函数,故该函数单调递增区间为(-1,1),减区间为[1,3].
(3)∵u=2x+3-x2=-(x-1)2+4≤4,
∴y=log4u≤log44=1.
故当x=1,u取最大值4时,y取最大值1.
15.(本小题满分8分)某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本.若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应的提高比例为0.75x,同时预计年销售量增加的比例为0.6x.
(1)写出本年度预计的年利润y与投入增加的比例x的关系式;
(2)为使本年度的年利润比上年有所增加,问投入成本增加的比例x应在什么范围内.
分析:年利润=(出厂价-投入成本)×年销售量.
解:(1)由题意,得y=[1.2(1+0.75x)-1×(1+x)]×1000(1+0.6x)(0<x<1).
整理,得y=-60x2+20x+200(0<x<1).
(2)要保证本年度的利润比上年度有所增加,只需
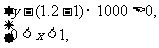 即
即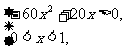
解得0<x<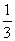 ,
,
即为保证本年度的利润比上年度有所增加,投入成本的比例应满足0<x<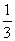 .
.
14.若函数f(x)=lg(x2+ax-a-1)在区间[2,+∞)上单调递增,则实数a的取值范围是_________.
解析:本题考查复合函数单调性的判定方法,要注意判断函数的单调性必须在函数的定义域内进行.
∵函数f(x)在区间[2,+∞)上单调递增,
∴-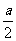 ≤2,且x=2时,x2+ax-a-1>0,即
≤2,且x=2时,x2+ax-a-1>0,即
 ∴
∴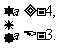
∴a>-3,即实数a的取值范围是(-3,+∞).
答案:(-3,+∞)
13.国家规定的个人稿酬纳税方法是:不超过800元的不纳税;超过800元而不超过4000元的按超过800元的14%纳税;超过4000元按全部稿酬的11%纳税.某人出版了一本书,共纳税420元,他的稿费为_______元.
解析:若其稿费为4000元,则应纳税3200×14%=448>420.
故稿费应小于4000元,设为x元.
则(x-800)14%=420,解得x=3800(元).
答案:3800
12.3log9(lg2-1)2+5log25(log0.5-2)2等于_________.
解析:3log9(log2-1)2+5log25(log0.5-2)2=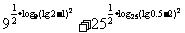 =9log9(1-lg2)+25log25(2-lg0.5)
=9log9(1-lg2)+25log25(2-lg0.5)
=1-lg2+2-lg0.5=3-lg(2×0.5)=3.
答案:3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com