
题目列表(包括答案和解析)
3.条件“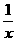 <1”是条件“x>1”的
<1”是条件“x>1”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析: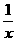 <1
<1
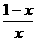 <0
<0 x>1或x<0,所以
x>1或x<0,所以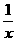 <1
<1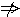 x>1;但x>1
x>1;但x>1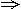
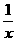 <1,所以"
<1,所以"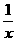 <1"是"x>1"的必要不充分条件.
<1"是"x>1"的必要不充分条件.
答案:B
2.方程x2-px+6=0的解集为M,方程x2+6x-q=0的解集为N,且M∩N={2},那么p+q等于
A.21 B.8 C.6 D.7
解析:由题意可知,2是方程x2-px+6=0且x2+6x-q=0的根,
所以22-2p+6=0,22+6×2-q=0.
解得p=5,q=16.
于是p+q=5+16=21.
答案:A
1.已知A={x|y=x,x∈R},B={y|y=x2,x∈R},则A∩B等于
A.{x|x∈R} B.{y|y≥0}
C.{(0,0),(1,1)} D.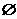
解析:∵集合A代表函数y=x的定义域,∴A=R;∵集合B代表函数y=x2的值域,
∴B={y|y≥0}.∴A∩B={y|y≥0}.
答案:B
19.(本小题满分12分)
某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元.销售单价与日均销售量的关系如下表所示:
|
销售单价/元 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
日均销售量/桶 |
480 |
440 |
400 |
360 |
320 |
280 |
240 |
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
解:根据上表,销售单价每增加1元,日均销售量就减少40桶.设在进价基础上增加x元后,日均销售利润为y元,而在此情况下的日均销售量为
480-40(x-1)=520-40x.
由于x>0,且520-40x>0,即0<x<13,
于是可得
y=(520-40x)x-200
=-40x2+520x-200,0<x<13.
易知,当x=-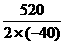 =6.5时,y有最大值.
=6.5时,y有最大值.
所以,只需将销售单价定为11.5元,就可获得最大的利润.
18.(本小题满分10分)已知函数f(x)对任意x、y∈R,都有f(x)+f(y)=f(x+y),且当x>0时,都有f(x)<0.
(1)求f(0);
(2)证明f(x)是R上的减函数.
(1)解:令x=y=0,则有f(0)+f(0)=f(0),∴f(0)=0.
(2)证明:设x1<x2,则x2-x1>0,f(x2)=f[x1+(x2-x1)]=f(x1)+f(x2-x1).
∵x2-x1>0,
∴f(x2-x1)<0.
∴f(x2)=f(x1)+f(x2-x1)<f(x1).∴f(x)是R上的减函数.
17.(本小题满分12分)已知函数y=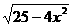 (x∈[0,
(x∈[0,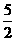 ]),
]),
(1)求它的反函数f-1(x);
(2)判断y=f-1(x)在其定义域上的单调性并证明.
解:(1)由y=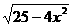 得x=±
得x=±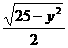 .
.
∵x∈[0,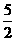 ],
],
∴x=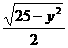 .
.
∴f-1(x)=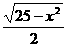 ,x∈[0,5].
,x∈[0,5].
(2)y=f-1(x)在其定义域[0,5]上是减函数.
证明:设0≤x1<x2≤5.
则f-1(x1)-f-1(x2)=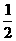 (
(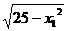 -
-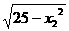 )=
)=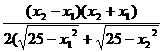 .
.
又∵0≤x1<x2≤5,∴x2-x1>0,x1+x2>0,
2(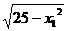 +
+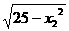 )>0.∴f-1(x1)>f-1(x2).∴y=f-1(x)在其定义域上是减函数.
)>0.∴f-1(x1)>f-1(x2).∴y=f-1(x)在其定义域上是减函数.
16.(本小题满分10分)设P:函数y=ax2-2x+1在[1,+∞)内单调递减,Q:曲线y=x2-2ax+4a+5与x轴没有交点.
如果P与Q有且只有一个正确,求a的取值范围.
解:由P知,a=0或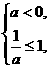 解得a≤0.由Q知Δ=(-2a)2-4(4a+5)<0,解得-1<a<5.
解得a≤0.由Q知Δ=(-2a)2-4(4a+5)<0,解得-1<a<5.
若P正确,Q不正确,则有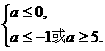 ∴a≤-1.
∴a≤-1.
若P不正确,Q正确,则有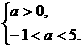 ∴0<a<5.
∴0<a<5.
综上可知,a的取值范围为a≤-1或0<a<5.
15.(本小题满分10分)作出下列函数的图象,并根据图象指出函数的值域.
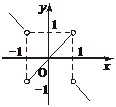
(1)y=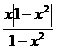 ;
;
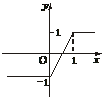
(2)y=|x|-|x-1|.
解:(1)y= 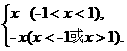
图象如下图.根据图象可知函数的值域为{y∈R|y≠1且y≠-1}.
(2)y= 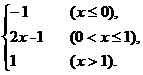
图象如下图.根据图象可知函数的值域为[-1,1].
14.设函数f(x)的反函数为h(x),函数g(x)的反函数为h(x+1),已知f(2)=5,f(5)=-2,f(-2)=8,那么g(2)、g(5)、g(8)、g(-2)中,一定能求出具体数值的是_______.
解析:由h(x)=f-1(x),h(x+1)=g-1(x),
∴g-1(x)=f-1(x+1)=y,
即x=g(y),x+1=f(y).
∴g(x)=f(x)-1.
∴g(2)=f(2)-1=4,g(5)=-3,g(-2)=7.
答案:g(2),g(5),g(-2)
13.若函数f(x)的图象关于原点对称,且f(x)在(0,+∞)上是增函数,f(-3)=0,则不等式xf(x)<0的解集为_______.
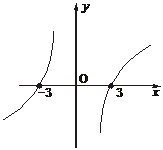
解析:由xf(x)<0得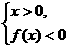 或
或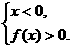 由上图进而得0<x<3或-3<x<0.
由上图进而得0<x<3或-3<x<0.
答案:(-3,0)∪(0,3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com