
题目列表(包括答案和解析)
2.在下边的列联表中,类Ⅰ中类B所占的比例为 ( A )
|
|
Ⅱ |
||
|
类1 |
类2 |
||
|
Ⅰ |
类A |
a |
b |
|
类B |
c |
d |
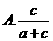
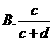
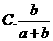
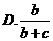
1.下列两个变量之间的关系哪个不是函数关系( D )
A.角度和它的正弦值 B.正方形边长和面积
C.正n边形边数和顶点角度之和 D.人的年龄和身高
22.如图,已知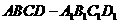 是棱长为3的正方体,点
是棱长为3的正方体,点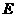 在
在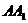 上,点
上,点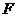 在
在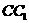 上,且
上,且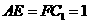 ,
,
(1)求证: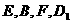 四点共面;(4分)
四点共面;(4分)
(2)若点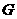 在
在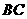 上,
上,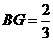 ,点
,点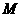 在
在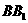 上,
上,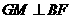 ,垂足为
,垂足为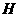 ,求证:
,求证: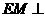 面
面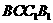 ;(4分)
;(4分)
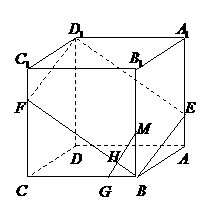 (3)用
(3)用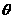 表示截面
表示截面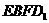 和面
和面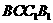 所成锐二面角大小,求
所成锐二面角大小,求 .(4分)
.(4分)
21.某安全生产监督部门对5家小型煤矿进行安全检查(简称安检).若安检不合格,则必须进行整改.若整改后经复查仍不合格,则强行关闭.设每家煤矿安检是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5, 整改后安检合格的概率是0.8,计算(结果精确到0.01): (1)恰好有两家煤矿必须整改的概率;
(2)至少关闭一家煤矿的概率.
20.甲、乙两名跳高运动员一次试跳2米高度成功的概率分别为0.7、0.6,且每次试跳成功与否相互之间没有影响,求: (1)甲试跳三次,第三次才能成功的概率;
(2)甲、乙两人在第一次试跳中至少有一人成功的概率; (3)甲、乙各试跳两次,甲比乙的成功次数恰好多一次的概率.
19.甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;乙袋装有2个红球,n个白球。现从甲、乙两袋中各任取2个球, (1)若n=3,求取到的4个球全是红球概率; (2)若取到的4个球中至少有2个红球的概率为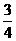 ,求n.
,求n.
18.用0,1,2,3,4,5这六个数字 (1)组成多少个无重复数字的五位奇数?
(2)可组成多少个无重复数字的能被5整除的五位数? (3)可组成多少个无重复数字的且大于31250的五位数?
17.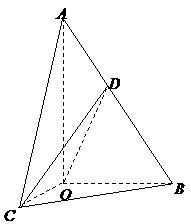 如图,在
如图,在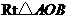 中,
中,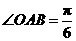 ,斜边
,斜边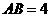 .
.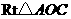 可以通过
可以通过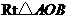 以直线
以直线 为轴旋转得到,且二面角
为轴旋转得到,且二面角 的直二面角.
的直二面角.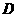 是
是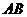 的中点. (I)求证:平面
的中点. (I)求证:平面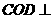 平面
平面 ;
;
(II)求异面直线 与
与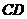 所成角的大小.
所成角的大小.
16.安排3名支教教师去4所学校任教,每校至多2人,则不同的分配方案有
种.(用数字作答)
15.在正方体上任意选择两条棱,则这两条棱相互平行的概率为 (用分数作答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com