
题目列表(包括答案和解析)
28、证明:(1)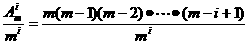 ,
,
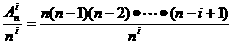 ,
,
对于m<n,当k=1,2,…,i-1,有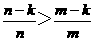
∴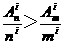 , ∴
, ∴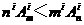 .
.
(2)由二项式定理:
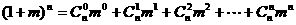
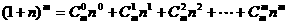
又∵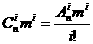 ,
,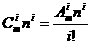 ,而
,而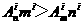
∴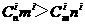 ∴
∴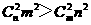 ,
,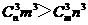 ,
,
……,
又∵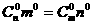 ,
, 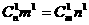
∴ .
.
27、解:(1)∵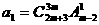
∴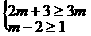 即
即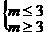
∴ m=3
由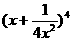 知:
知: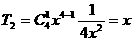
∴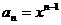 ,
,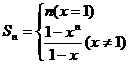
(2)当x=1时,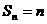 .
.
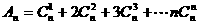 .
.
∴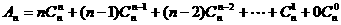 .
.
两式相加得: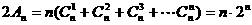 .
.
∴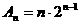 .
.
当x≠1时,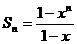 .
.
∴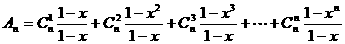
=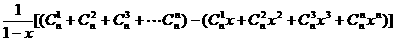
=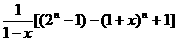
=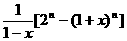
综上,得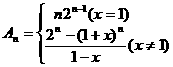 .
.
25、 B
26、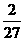
24.证明:⑴设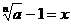 ,则
,则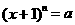 ,
,
∴原不等式等价于: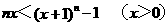
∵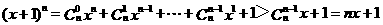
∴原不等式成立.
⑵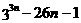
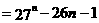
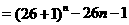
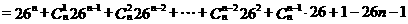

∵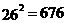
∴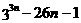 都可被676整除.
都可被676整除.
C组答案
23.解:⑴由要求知:5只能在个位,故能被5整除的三位数有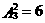 个
个
⑵当0在个位时,三位数有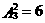 个
个
当2或4在个位是,三位数有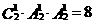 个
个
∴当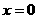 时,三位偶数共有
时,三位偶数共有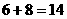 个
个
⑶易知: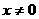
∵1,2,4,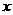 在各个数位上出现的次数都相同,且各自出现
在各个数位上出现的次数都相同,且各自出现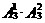 次
次
∴数字之和为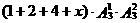
∴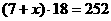 ,解得
,解得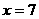 .
.
22.解:原不等式化为: 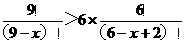
解得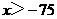
又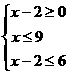 得
得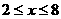 且
且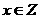
∴原不等式的解集为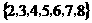 .
.
12、解:∵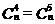 ,∴
,∴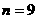
∴在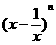 中,
中,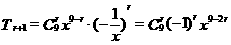
令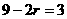 得
得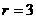
∴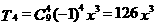 ,
,
∴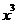 的系数是126.
的系数是126.
B组答案:
13-17:BDBAC 18.84 19.36 20.24789 21.15
11、解:⑴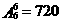 ,∴男生甲排在正中间的排法有720种;
,∴男生甲排在正中间的排法有720种;
⑵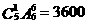 ,∴男生甲不排在两端的排法有3600种;
,∴男生甲不排在两端的排法有3600种;
⑶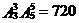 ,∴三个女生排在一起的排法有720种;
,∴三个女生排在一起的排法有720种;
⑷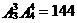 ,∴三个女生两两都不相邻的排法有144种.
,∴三个女生两两都不相邻的排法有144种.
10、解:⑴原式= 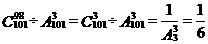
⑵由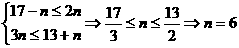
∴原式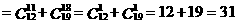
28、(本题18分)
已知i、m、n是正整数,且1<i≤m<n .
(1)证明: ;
;
(2)证明:(1+m)n>(1+n)m .
厦门市2007-2008学年选修2-3练习(一)答案
A组答案
1-5. ABCCB 6.1540 7.20 8.256 9.-160
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com