
题目列表(包括答案和解析)
5.函数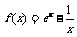 (其中
(其中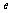 为自然对数的底数)的零点所在的区间是( )
为自然对数的底数)的零点所在的区间是( )
A.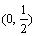 B.
B.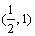 C.
C.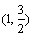 D.
D.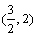
4. 设向量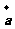 与
与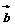 的夹角为
的夹角为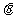 ,
,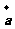 =(2,1),3
=(2,1),3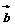 +
+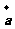 =(5,4),则
=(5,4),则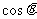 = ( )
= ( )
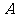 .
.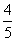
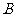 .
. 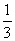
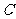 .
.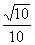
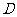 .
.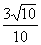
3.已知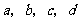 成等比数列,且曲线
成等比数列,且曲线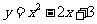 的顶点是
的顶点是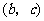 ,则
,则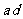 等于( )
等于( )
A.3 B.2 C.1 D.
2.若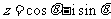 (i为虚数单位),则使
(i为虚数单位),则使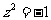 的
的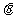 值可能是( )
值可能是( )
A.0 B.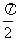 C.
C.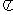 D.
D.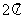
1. 设函数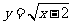 的定义域为集合M,集合N=
的定义域为集合M,集合N=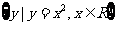 ,则
,则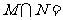 ( ).
( ).
A.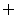 B.N C.
B.N C.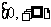 D.M
D.M
本试卷共150分,120分钟完成,答案写在答题卷上。
第Ⅰ卷
20.(本小题满分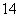 分)
分)
设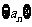 是由非负整数组成的数列,且满足
是由非负整数组成的数列,且满足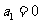 ,
,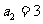 ,
,
 ,
,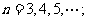
(1)求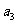 ;
;
(2)证明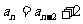 ,
,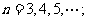
(3)求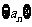 的通项公式。
的通项公式。
附加题(本题为附加题,如果解答正确,加5 分,但全卷总分不超过150分)
若存在实常数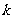 和
和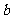 ,使得函数
,使得函数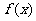 和
和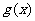 对其定义域上的任意实数
对其定义域上的任意实数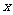 分别满足:
分别满足: 和
和 ,则称直线
,则称直线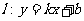 为
为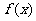 和
和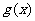 的“隔离直线”.
的“隔离直线”.
已知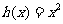 ,
,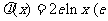 为自然对数的底数).问:
为自然对数的底数).问:
函数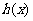 和
和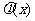 是否存在“隔离直线”?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在“隔离直线”?若存在,求出此隔离直线方程;若不存在,请说明理由.
19.(本小题满分14分)
某电视台举行电视奥运知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,
初赛采用选手选一题答一题的方式进行,每位选手最多有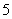 次选题答题的机会,选手累计答对
次选题答题的机会,选手累计答对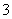 题或答错
题或答错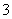 题即终止其初赛的比赛,答对
题即终止其初赛的比赛,答对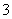 题者直接进入决赛,答错
题者直接进入决赛,答错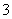 题者则被淘汰.已知选手甲答题的正确率为
题者则被淘汰.已知选手甲答题的正确率为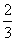 .
.
(1) 求选手甲可进入决赛的概率;
(2) 设选手甲在初赛中答题的个数为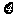 ,试写出
,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.
18.(本小题满分14分)
已知函数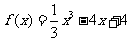 ,
,
(1)求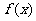 的单调区间;
的单调区间;
(2)求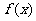 在
在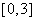 上的最大值和最小值。
上的最大值和最小值。
17.(本小题满分14分)
在二项式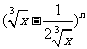 的展开式中,
的展开式中,
(1)若所有二项式系数之和为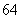 ,求展开式中二项式系数最大的项.
,求展开式中二项式系数最大的项.
(2)若前三项系数的绝对值成等差数列,求展开式中各项的系数和。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com