
3.在等差数列{ }中,若
}中,若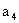 +
+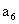 =12,
=12,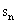 是数列{
是数列{ }的前n项和,则
}的前n项和,则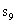 的值为( )
的值为( )
A. 48 B.54 C.60 D.66
2.设m、n是两条不同的直线,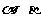 是两个不同的平面,考查下列命题,其中正确的命题是( )
是两个不同的平面,考查下列命题,其中正确的命题是( )
A.m⊥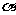 ,n
,n
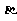 ,m⊥n
,m⊥n
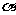 ⊥
⊥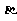
B.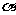 ∥
∥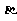 ,m⊥
,m⊥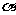 ,n∥
,n∥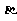
 m⊥n
m⊥n
C.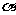 ⊥
⊥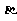 ,m⊥
,m⊥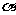 ,n∥
,n∥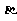
 m⊥n
m⊥n
D.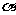 ⊥
⊥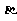 ,
,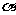 ∩
∩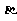 =m,n⊥m
=m,n⊥m n⊥
n⊥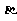
1.设集合M={x| 0<x≤3},N={x|O<x≤2},那么“a∈M”是“a∈N”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
22.(本题14分)
已知有穷数列{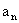 }共有2p项(整数p≥2),首项a1=2,该数列的前n项和为
}共有2p项(整数p≥2),首项a1=2,该数列的前n项和为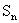 ,且
,且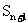 =a
=a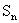 十2(1,2,……,2p-1),其中常数a>1.
十2(1,2,……,2p-1),其中常数a>1.
(1)求证:数列{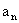 }是等比数列;
}是等比数列;
(2)若a=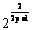 ,数列{
,数列{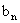 }满足
}满足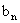 =
=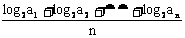 (n=1,2,……,2p),求数列{
(n=1,2,……,2p),求数列{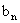 }的通项公式.
}的通项公式.
(3)在(2)的条件下,令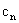 =|
=|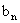 -
-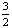 |且:C1+C2+……+C2p≤4,求p的值
|且:C1+C2+……+C2p≤4,求p的值
21.(本题12分)



 已知圆M:(x+
已知圆M:(x+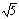 )2+y2=36,定点N(
)2+y2=36,定点N(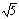 ,0),点P为圆M上的动点,点Q在NP上,点G在MP上,且满足NP=2 NQ,GQ·NP=0.
,0),点P为圆M上的动点,点Q在NP上,点G在MP上,且满足NP=2 NQ,GQ·NP=0.
(1)求点G的轨迹C的方程;




 (2)过点(2,0)作直线l与曲线C交于A、B两点,0是坐标原点,设OS=OA+OB,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
(2)过点(2,0)作直线l与曲线C交于A、B两点,0是坐标原点,设OS=OA+OB,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
20.(本题12分)
某学校为了解决教师住房问题,计划征用一块土地,盖一幢总建筑面积为am2的宿舍楼.已知土地的征用费为2388元/m2,且每层的建筑面积相同,土地的征用面积为第一层的2.5倍,经工程技术人员核算,第一、二层的建筑费用相同,费用为445元/m2,以后每增高一层,其建筑费用就增加30元/m2.试设计这幢宿舍楼的楼高层数,使总费用最少,并求其最少总费用(总费用为建筑费用和征地费用之和).
19. (本题12分)
(本题12分)
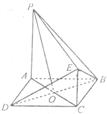
如图,已知正方形ABCD的边长为2,中心为O.设PA⊥平面ABCD,EC∥PA,且PA=2.
(1)当CE为多少时,PO⊥平面BED;
(2)在(1)的情形下,求二面角E-PB-A的余弦值.
18.(本题12分)
已知函数f(x)= 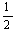 x2-alnx(a∈R)
x2-alnx(a∈R)
(1)求函数f(x)的单调区间;
(2)求证:x>1时,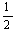 x2+lnx<
x2+lnx<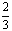 x3
x3
17.
 (本题12分)
(本题12分)


 若 a
若 a =(
=(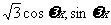 ), b=(sin
), b=(sin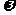 x,0),其中
x,0),其中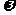 〉0,记函数f(x)=(a+b) ·
〉0,记函数f(x)=(a+b) ·
b +k
(1)若f(x)图象中相邻两条对称轴间的距离不小于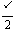 ,求
,求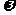 的取值范围.
的取值范围.
(2)若f(x)的最小正周期为丌,且当x∈[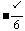 ,
,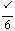 ]时,f(x)的最大值是
]时,f(x)的最大值是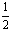 ,求f(x)的解析式。
,求f(x)的解析式。
16.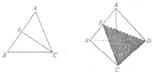 在平面几何中,△ABC的∠C内角平分线CE分AB所成线段的比|AE|:| EB|=| AC|:| CB|.把这个结论类比到空间:在三棱锥A-BCD中(如图),平面CDE平分二面角A-CD-B且与AB相交于E,可类比得到结论______
在平面几何中,△ABC的∠C内角平分线CE分AB所成线段的比|AE|:| EB|=| AC|:| CB|.把这个结论类比到空间:在三棱锥A-BCD中(如图),平面CDE平分二面角A-CD-B且与AB相交于E,可类比得到结论______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com