
题目列表(包括答案和解析)
16解:(Ⅰ)由图得
|
X |
(0,1) |
1 |
(1,2) |
2 |
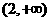 |
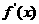
|
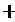 |
0
|
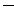 |
0 |
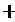
|
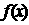 |
  |
极大值 |
 |
极小值 |

|
故当x (0, 1)时,f(x)是增函数,当 x
(0, 1)时,f(x)是增函数,当 x (2,,+∞)时,f(x)也是增函数,
(2,,+∞)时,f(x)也是增函数,
当x (1 ,2)时,f(x)是减函数. ……………………………5分
(1 ,2)时,f(x)是减函数. ……………………………5分
则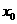 =1; ……………………………7分
=1; ……………………………7分
(Ⅱ)依题意得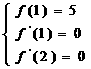 ……………10分 即
……………10分 即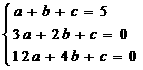

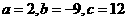 .……………………………13分
.……………………………13分
17、解:(Ⅰ)求导得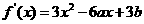 。……………………………1分
。……………………………1分
由于 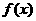 的图像与直线
的图像与直线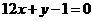 相切于点
相切于点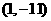 ,所以
,所以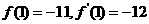 ,……3分
,……3分
即: 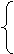 1-3a+3b = -11 解得:
1-3a+3b = -11 解得: 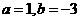 .…………6分
.…………6分
3-6a+3b=-12
(Ⅱ)由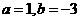 得:
得: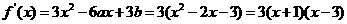 ……7分
……7分
令f′(x)>0,解得 x<-1或x>3;………9分,又令f′(x)< 0,解得 -1<x<3. ……10分
故当x (
(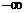 , -1)时,f(x)是增函数,当 x
, -1)时,f(x)是增函数,当 x (3,
(3, )时,f(x)也是增函数,………………12分
)时,f(x)也是增函数,………………12分
当x (-1 ,3)时,f(x)是减函数. ……………………………13分
(-1 ,3)时,f(x)是减函数. ……………………………13分
21.(本小题满分14分)
已知函数f(x)=x3+2x2+x-4,g(x)=ax2+x-8.
(1)若对任意x∈[0,+∞),都有f(x)≥g(x),求实数a的取值范围;
(2)若对任意的x1、x2∈[0,+∞),都有f(x1)≥g(x2),求实数a的取值范围.
(草稿纸)
 厦门六中2010届高二下月考数学(理科)参考答案及评分标准2009.3
厦门六中2010届高二下月考数学(理科)参考答案及评分标准2009.3
20. (本题满分14分)
已知函数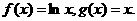
(1)求函数y=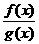 的最大值;
的最大值;
(2)若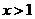 ,求证:
,求证: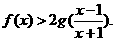
19.(本小题满分13分)
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量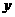 (升)关于行驶速度
(升)关于行驶速度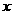 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: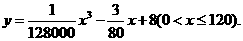 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
18. (本小题满分13分)已知函数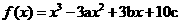 在
在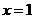 与x=3时都取得极值。
与x=3时都取得极值。
(1)求a、b之值与函数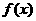 的单调区间;
的单调区间;
(2)若对任意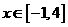 ,
,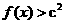 恒成立。求c的取值范围。
恒成立。求c的取值范围。
16.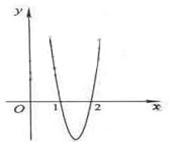 (本小题满分13分)
(本小题满分13分)
已知函数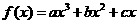 的定义域为
的定义域为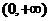 ,且在点
,且在点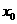 处取得极大值
处取得极大值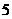 ,其导函数
,其导函数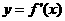 的图象经过点
的图象经过点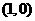 ,
,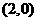 ,如图所示.
,如图所示.
(Ⅰ)讨论函数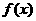 的单调性,并求
的单调性,并求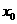 的值;
的值;
(Ⅱ)求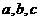 的值.
的值.
17(本小题满分13分)设函数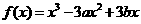 的图像与直线
的图像与直线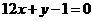 相切于点(1,-11)。
相切于点(1,-11)。
(Ⅰ)求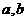 的值;
的值;
(Ⅱ)讨论函数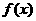 的单调性。
的单调性。
15.已知函数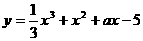 的单调递减区间是(-3,1),则
的单调递减区间是(-3,1),则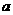 的值是
.
的值是
.
14.以初速度40m/s垂直向上抛一物体,ts时刻的速度为v=40-10t(单位:m/s),物体上抛的最大高度是 米。
13.由直线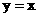 ,x=2,曲线
,x=2,曲线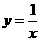 所围图形的面积为 。
所围图形的面积为 。
12.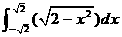 = 。
= 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com