
题目列表(包括答案和解析)
20.(本题满分12分)
解:(1)函数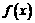 的定义域是
的定义域是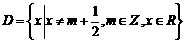 ,图像如图所示;
,图像如图所示;
(2)由于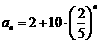 ,所以
,所以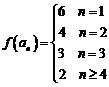 ,因此
,因此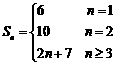 ;
;
(3)由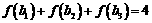 得
得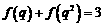 ,
,
当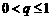 时,则
时,则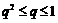 ,所以
,所以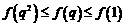 ,因为
,因为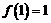 ,所以不合题意;
,所以不合题意;
 当
当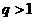 时,则
时,则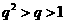 ,即
,即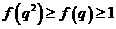 ,所以只可能是
,所以只可能是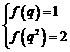 ,
,
 即
即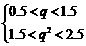 ,解得
,解得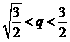 .
.
19.(本题满分12分)
解:(1)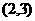 ⊙
⊙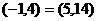
(2)设 中的任意三个元素
中的任意三个元素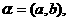
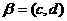 ,
,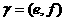
交换律: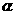 ⊙
⊙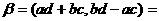
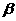 ⊙
⊙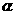
结合律:(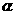 ⊙
⊙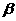 )⊙
)⊙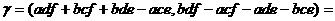
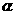 ⊙(
⊙(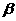 ⊙
⊙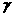 )
)
(3)假设存在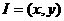 ,
,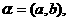 则
则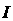 ⊙
⊙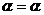 ,即
,即
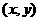 ⊙
⊙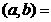
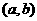
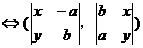
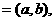
则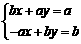 对任意实数a、b恒成立
对任意实数a、b恒成立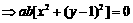 Þ
Þ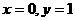
所以,存在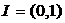 满足:对于任意
满足:对于任意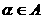 ,都有
,都有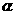 ⊙
⊙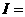
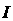 ⊙
⊙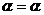 成立
成立
18.(本题满分12分)
解:(1)
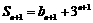 ,依题意,
,依题意,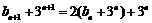
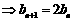
且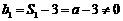 ,所以,数列
,所以,数列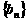 为公比为2的等比数列。
为公比为2的等比数列。
(2)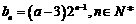 Þ
Þ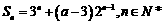
于是,当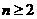 时,
时,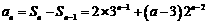
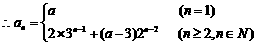
(3)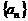 单调递增
单调递增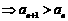 对所有正整数n均成立。首先,
对所有正整数n均成立。首先,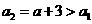
当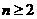 时,
时,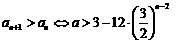
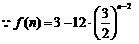 在
在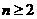 且nÎN上递减,\
且nÎN上递减,\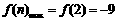
综上,所求的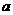 的取值范围是
的取值范围是
解: 
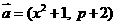 ,
,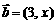 ,∴
,∴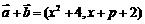 ,
,
又
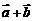 与
与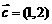 平行,∴
平行,∴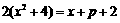 ,即
,即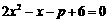 ,
,
由题意知方程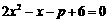 有两个相等的实根,
有两个相等的实根,
∴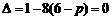 ,∴
,∴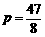 .
.
17.(本题满分8分)
解:(1)设N点坐标为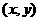 ,则M、P两点的坐标为
,则M、P两点的坐标为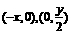
因为PM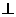 PF,所以
PF,所以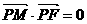 ,所以
,所以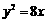 (x>0)
(x>0)
(2)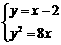
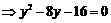 ,
,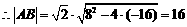 ,
,
而点O到直线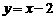 的距离
的距离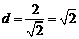 ,于是
,于是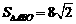 .
.
15.( C )
14.(B )
13.( A )
11.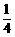 ,
,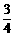 ;
;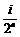 ,i为[1,2n]中的所有奇数
,i为[1,2n]中的所有奇数
二、12.( D )
10.;-2
9. 4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com