
题目列表(包括答案和解析)
3.(2005年黄冈市调研题)如果方程 +
+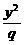 =1表示双曲线,则下列椭圆中,与该双曲线共焦点的是
=1表示双曲线,则下列椭圆中,与该双曲线共焦点的是
A.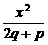 +
+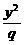 =1
B.
=1
B.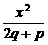 +
+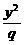 =-1
=-1
C.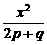 +
+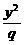 =1
D.
=1
D.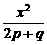 +
+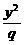 =-1
=-1
解析:由题意有pq>0,若p>0,q>0,则双曲线焦点位于y轴上且c2=p+q无答案,则只有p<0,q<0,焦点位于x轴上,且c2=-p-q,B答案符合.
答案:B
|
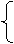 x=2cosθ,
x=2cosθ,
y=sinθ(其中参数θ∈R)上的点的最短距离为
A.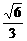 B.1
C.
B.1
C. 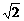 D.
D. 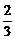
解析:d=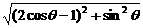
=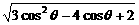
=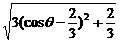 ,
,
dmin=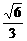 .
.
答案:A
2.(2005年启东市第二次调研题)过点M(-2,0)的直线l与椭圆x2+2y2=2交于P1、P2两点,线段P1P2的中点为P,设直线l的斜率为k1(k1≠0),直线OP的斜率为k2,则k1·k2的值为
A.2 B.-2
C.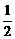 D.-
D.-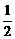
解析:设P1(x1,y1)、P2(x2,y2),中点P(x0,y0),则k1= ,k2=
,k2=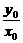 =
= .
.
将P1、P2两点坐标代入椭圆方程x2+2y2=2,相减得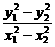 =-
=-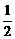 .
.
∴k1·k2= ·
· =
=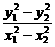 =-
=-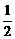 .
.
答案:D
1.过原点的直线l与双曲线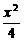 -
-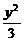 =-1交于两点,则直线l的斜率的取值范围是
=-1交于两点,则直线l的斜率的取值范围是
A.(-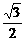 ,
,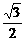 )
)
B.(-∞,-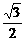 )∪(
)∪(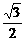 ,+∞)
,+∞)
C.[-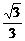 ,
,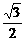 ]
]
D.(-∞,-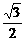 )∪[
)∪[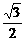 ,+∞)
,+∞)
解析:双曲线焦点在y轴上,渐近线斜率为±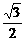 ,利用数形结合易得k>
,利用数形结合易得k>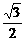 或k< -
或k< -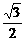 .
.
答案:B
22.(14分)如图,ABCD是边长为1的正方形,M、N分别是DA、BC上的点,且MN∥AB,现沿MN折成直二面角AB-MN-CD.
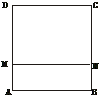
(1)求证:平面ADC⊥平面AMD;
(2)设AM=x(0<x<1),MN到平面ADC的距离为y,试用x表示y;
(3)点M在什么位置时,y有最大值,最大值为多少?
(1)证明:∵ABCD是正方形,且MN∥AB∥CD,∴MN⊥AM,MN⊥DM,即CD⊥AM,CD⊥DM,∴CD⊥平面AMD.
∵CD 平面ADC,
平面ADC,
∴平面ADC⊥平面AMD.
(2)解:∵MN∥CD,∴MN∥平面ADC.故MN到平面ADC的距离即为M到平面ADC的距离.过M作MH⊥AD于H,∵平面ADC⊥平面AMD,
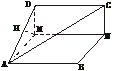
∴MH⊥平面ADC,即MH为所求距离.
在Rt△AMD中,求得y=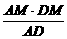 =
=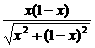 (0<x<1).
(0<x<1).
(3)解:y≤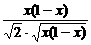 =
=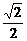
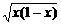 ≤
≤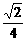 ,当且仅当x=1-x,即x=
,当且仅当x=1-x,即x=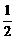 时,ymax=
时,ymax=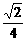 ,此时M为AD的中点.
,此时M为AD的中点.
21.(12分)已知四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为菱形,∠BAD=60°,AB=2,PA=4,E为PC的中点.
(1)求证:平面BDE⊥平面ABCD;
(2)求二面角B-DE-C的大小.
(1)证明:设AC∩BD=O,连结OE.
∵E为PC的中点,O为AC的中点.
∴EO∥PA.
∵PA⊥面ABCD,∴EO⊥面ABCD.
∵EO 平面BDE,∴面BDE⊥面ABCD.
平面BDE,∴面BDE⊥面ABCD.
(2)解法一:过O作OF⊥DE于F,连结CF.
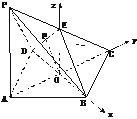
由(1)可知OC⊥面BDE,
∴DE⊥FC.
∴∠OFC为B-DE-C的平面角.
∵OE=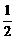 PA=2,OD=1,∴OF=
PA=2,OD=1,∴OF=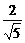 .
.
又∵OC= ,∴tan∠OFC=
,∴tan∠OFC=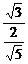 =
=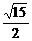 .
.
∴二面角B-DE-C的大小为arctan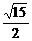 .
.
解法二:以O为原点建立如上图所示的坐标系,则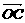 为平面EBD的法向量,
为平面EBD的法向量,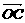 =(0,
=(0, ,0).
,0).
设平面CDE的法向量n=(x,y,z).
∵E(0,0,2),C(0, ,0),D(-1,0,0),
,0),D(-1,0,0),
∴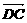 =(1,
=(1, ,0),
,0),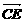 =(0,-
=(0,- ,2).
,2).
∵n·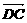 =0,n·
=0,n·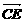 =0,
=0,
|
|
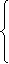
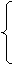 x+
x+ y=0, x=-
y=0, x=- y,
y,
- y+2z=0. z=
y+2z=0. z=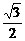 y.
y.
取y= ,则n=(-3,
,则n=(-3, ,
,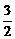 ).∴cos〈n,
).∴cos〈n,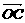 〉=
〉=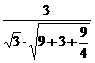 =
=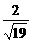 .
.
∴二面角B-DE-C的大小为arccos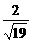 .
.
20.(12分)(理)如图,已知矩形ABCD,PA⊥平面ABCD,M、N分别是AB、PC的中点,设AB=a,BC=b,PA=c.
(1)建立适当的空间直角坐标系,写出A、B、M、N点的坐标,并证明MN⊥AB;
(2)平面PDC和平面ABCD所成的二面角为θ,当θ为何值时(与a、b、c无关),MN是直线AB和PC的公垂线段.
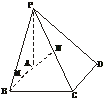
(1)证明:以A为原点,分别以AB、AD、AP为x轴、y轴、z轴,建立空间直角坐标系.
则A(0,0,0),B(a,0,0),M( ,0,0),N(
,0,0),N( ,
,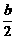 ,
,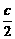 ).
).
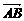 =(a,0,0),
=(a,0,0),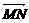 =(0,
=(0,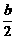 ,
,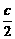 ).
).
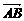 ·
·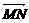 =0
=0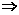 AB⊥MN.
AB⊥MN.
(2)解:P(0,0,c),C(a,b,0),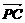 =(a,b,-c),若MN是PC、AB的公垂线段,则
=(a,b,-c),若MN是PC、AB的公垂线段,则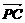 ·
·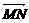 =0,即-
=0,即-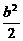 +
+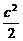 =0
=0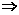 b=c.
b=c.
|
 又∵AP⊥面ABCD
又∵AP⊥面ABCD
CD⊥DA
∴∠PDA是二面角P-CD-A的平面角.
∴∠PDA=45°,
即二面角P-CD-A是45°.
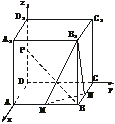
(文)正方体ABCD-A1B1C1D1中,M、N、P分别为棱AB、BC、DD1的中点.
(1)求证:PB⊥平面MNB1;
(2)设二面角M-B1N-B为α,求cosα的值.
(1)证明:如图,以D为原点,DA、DC、DD1分别为x轴、y轴、z轴建立空间直角坐标系,取正方体棱长为2,则P(0,0,1)、M(2,1,0)、B(2,2,0)、B1(2,2,2).
∵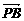 ·
·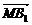 =(2,2,-1)·(0,1,2)=0,
=(2,2,-1)·(0,1,2)=0,
∴MB1⊥PB,同理,知NB1⊥PB.
∵MB1∩NB1=B1,∴PB⊥平面MNB1.
(2)∵PB⊥平面MNB1,BA⊥平面B1BN,∴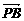 =(2,2,-1)与
=(2,2,-1)与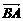 =(0,2,0)所夹的角即为α,cosα=
=(0,2,0)所夹的角即为α,cosα=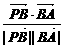 =
=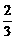 .
.
19.(12分)(2005年春季上海,19)已知正三棱锥P-ABC的体积为72 ,侧面与底面所成的二面角的大小为60°.
,侧面与底面所成的二面角的大小为60°.
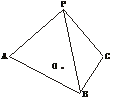
(1)证明:PA⊥BC;
(2)求底面中心O到侧面的距离.
(1)证明:取BC边的中点D,连结AD、PD,则AD⊥BC,PD⊥BC,故BC⊥平面APD.
∴PA⊥BC.
(2)解:如下图,由(1)可知平面PBC⊥平面APD,则∠PDA是侧面与底面所成二面角的平面角.
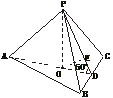
过点O作OE⊥PD,E为垂足,则OE就是点O到侧面的距离.
设OE为h,由题意可知点O在AD上,
∴∠PDO=60°,OP=2h,OD=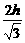 .
.
∴BC=4h.
∴S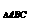 =
=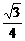 (4h)2=4
(4h)2=4 h2.
h2.
∵72 =
= 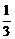 ·4
·4 h2·2h=
h2·2h=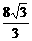 h3,∴h=3,
h3,∴h=3,
即底面中心O到侧面的距离为3.
18.(12分)(2004年广东,18)如下图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E、F分别是线段AB、BC上的点,且EB=FB=1.
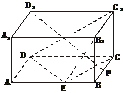
(1)求二面角C-DE-C1的正切值;
(2)求直线EC1与FD1所成角的余弦值.
解:(1)以A为原点,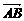 、
、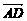 、
、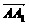 分别为x轴、y轴、z轴的正向建立空间直角坐标系,则有D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4,3,2).
分别为x轴、y轴、z轴的正向建立空间直角坐标系,则有D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4,3,2).
于是,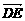 =(3,-3,0),
=(3,-3,0),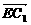 =(1,3,2),
=(1,3,2),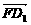 =(-4,2,2).
=(-4,2,2).
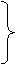


 设向量n=(x,y,z)与平面C1DE垂直,则有 n⊥
设向量n=(x,y,z)与平面C1DE垂直,则有 n⊥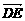 3x-3y=0
3x-3y=0
n⊥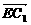 x+3y+2z=0
x+3y+2z=0
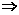 x=y=-
x=y=-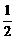 z.
z.
∴n=(-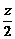 ,-
,-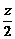 ,z)=
,z)=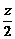 (-1,-1,2),其中z>0.
(-1,-1,2),其中z>0.
取n0=(-1,-1,2),则n0是一个与平面C1DE垂直的向量.
∵向量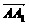 =(0,0,2)与平面CDE垂直,
=(0,0,2)与平面CDE垂直,
∴n0与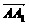 所成的角θ为二面角C-DE-C1的平面角.
所成的角θ为二面角C-DE-C1的平面角.
∴cosθ=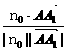 =
=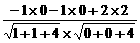 =
=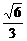 .
.
∴tanθ=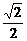 .
.
(2)设EC1与FD1所成的角为β,则
cosβ= =
=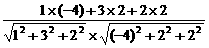 =
=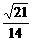 .
.
17.(12分)(2003年上海)已知平行六面体ABCD-A1B1C1D1中,A1A⊥平面ABCD,AB=4,AD=2.若B1D⊥BC,直线B1D与平面ABCD所成的角等于30°,求平行六面体ABCD-A1B1C1D1的体积.
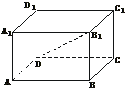
解:连结BD,
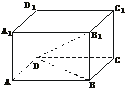
∵B1B⊥平面ABCD,B1D⊥BC,∴BC⊥BD.
在△BCD中,BC=2,CD=4,∴BD=2 .
.
又∵直线B1D与平面ABCD所成的角等于30°,
∴∠B1DB=30°.
于是BB1=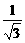 BD=2.
BD=2.
故平行六面体ABCD-A1B1C1D1的体积为S ABCD·BB1=8
ABCD·BB1=8 .
.
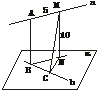
16.已知异面直线a、b的公垂线段AB的长为10 cm,点A、M在直线a上,且AM=5 cm,若直线a、b所成的角为60°,则点M到直线b的距离是__________.
解析:如图,过B作BN∥a,且BN与b确定的平面为α,过M作MN⊥α于N,过N作NC⊥b于C,连结MC,由三垂线定理知,MC⊥b,故MC即为所求.在Rt△BCN中,NC=BNsin60°=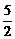
 ,
,
∴MC=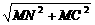 =
=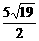 .
.
答案: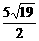
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com