
题目列表(包括答案和解析)
1、能够把研究直线与圆锥曲线位置关系的问题转化为研究方程组的解的问题;
18.(本小题满分12分)
(Ⅰ)依题意,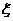 的可能取值为2,3,4 ……………1分
的可能取值为2,3,4 ……………1分
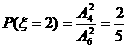 ; ……………3分
; ……………3分
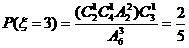 ; ……………5分
; ……………5分
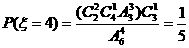 ; ……………7分
; ……………7分
∴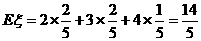 . 故取球次数
. 故取球次数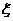 的数学期望为
的数学期望为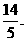 ……8分
……8分
(Ⅱ)依题意,连续摸4次球可视作4次独立重复试验,且每次摸得红球的概率均为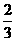 ,
,
则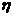 -
-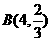 , ……………10分
, ……………10分
∴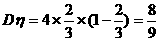 . 故共取得红球次数
. 故共取得红球次数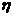 的方差为
的方差为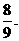 ……12分
……12分
18(本小题满分12分)
在一段线路中有4个自动控制的常用开关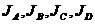 如图连接在一起
如图连接在一起 假定在某年第一季度开关
假定在某年第一季度开关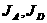 能够闭合的概率都是0
能够闭合的概率都是0 7,开关
7,开关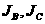 能够闭合的概率都是0
能够闭合的概率都是0 8
8
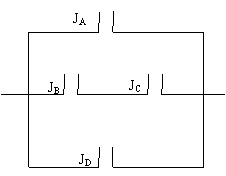 (1)求
(1)求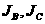 所在线路能正常工作的概率;
所在线路能正常工作的概率;
(2)计算在第一季度这段线路能正常工作的概率
18(本小题满分12分)
解设开关JA,JB ,JC ,JD 能够闭合的事件依次为A B
B C
C D,则P(A)=P(D)=0
D,则P(A)=P(D)=0 7,P(B)=P(C)=0
7,P(B)=P(C)=0 8
8
(1)P(B C)=P(B)
C)=P(B) P(c)=0
P(c)=0 8╳0
8╳0 8=0
8=0 64…………………6分
64…………………6分
(2)JA不能工作的概率为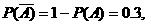
JD不能工作的概率为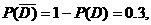 --------8分
--------8分
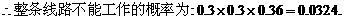 --------10分
--------10分
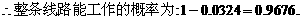
所以整条线路能正常工作的概率为0 9676----------------------12分
9676----------------------12分
答:9月份这段线路能正常工作的概率为0 9676
9676 …………………14分
…………………14分
18.(本小题满分12分)
已知袋中装有大小相同的2个白球和4个红球.
(Ⅰ)从袋中随机地将球逐个取出,每次取后不放回,直到取出两个红球为止,求取球次数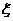 的数学期望;
的数学期望;
(Ⅱ)从袋中随机地取出一个球,放回后再随机地取出一个球,这样连续取4次球,求共取得红球次数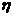 的方差.
的方差.
19.解 (Ⅰ)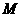 点到达点
点到达点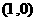 的概率为
的概率为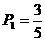 ;
;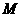 点到达点
点到达点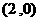 的事件由两个互斥事件组成:①A=“
的事件由两个互斥事件组成:①A=“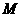 点先按向量
点先按向量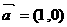 到达点
到达点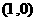 ,再按向量
,再按向量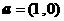 到达点
到达点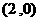 ”,此时
”,此时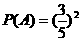 ;
;
②B=“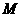 点先按向量
点先按向量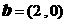 移动直接到达点
移动直接到达点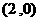 ”,此时
”,此时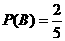 。
。
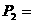
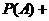
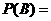
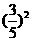
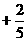
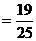
(Ⅱ) 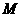 点到达点
点到达点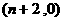 的事件由两个互斥事件组成:
的事件由两个互斥事件组成:
①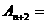 “从点
“从点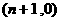 按向量
按向量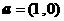 移动到达点
移动到达点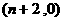 ”,
”,
此时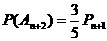 ;
;
②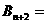 “从点
“从点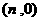 按向量
按向量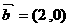 移动到达点
移动到达点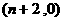 ”,此时
”,此时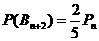 。
。
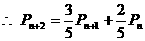 ,即
,即 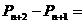
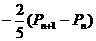
 数列
数列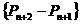 是以
是以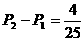 为首项,公比为
为首项,公比为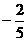 的等比数列。
的等比数列。
(Ⅲ)由(Ⅱ)可知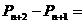
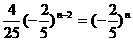
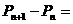
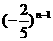
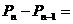
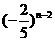
……
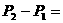
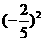
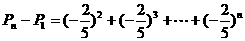
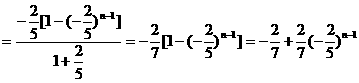
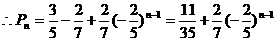
19.(本小题14分)
从原点出发的某质点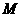 ,按照向量
,按照向量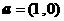 移动的概率为
移动的概率为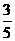 ,按照向量
,按照向量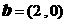 移动的概率为
移动的概率为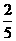 ,设可到达点
,设可到达点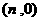 的概率为
的概率为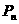 .
.
(Ⅰ)求概率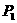 、
、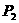 ;
;
(Ⅱ)求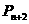 与
与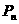 、
、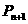 的关系并证明数列
的关系并证明数列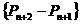 是等比数列;
是等比数列;
(Ⅲ)求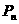 .
.
17、(1)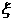 的所有可能取值为2450,1450,450,-550 ,
的所有可能取值为2450,1450,450,-550 ,
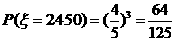
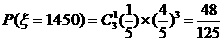
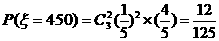
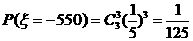 ,
,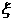 分布列为
分布列为
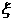 |
2450 |
1450 |
450 |
-550 |
|
P |
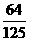 |
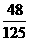 |
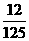 |
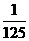 |
…(6分)
(2)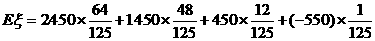
=1850(元)) …(9分)
设小李不出资50元增加1张奖券消费的实际支出为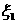 (元)
(元)
则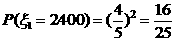
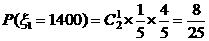
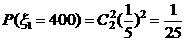
∴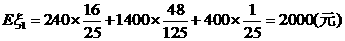
∴
故小王出资50元增加1张奖券划算。…(12分)
17.(本小题满分12分)
移动公司进行促销活动,促销方案为顾客消费1000元,便可获得奖券一张,每张奖券中奖的概率为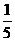 ,中奖后移动公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为
,中奖后移动公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为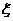 (元).
(元).
(1)求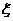 的分布列;
的分布列;
(2)试说明小李出资50元增加1张奖券是否划算。
17.(本小题满分12分)在一次军事演习中,某军同时出动了甲、乙、丙三架战斗机对一军事目标进行轰炸,已知甲击中目标的概率是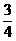 ;甲、丙同时轰炸一次,目标未被击中的概率为
;甲、丙同时轰炸一次,目标未被击中的概率为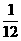 ;乙、丙同时轰炸一次,都击中目标的概率是
;乙、丙同时轰炸一次,都击中目标的概率是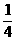 .(1)求乙、丙各自击中目标的概率;(2)求目标被击中的概率.
.(1)求乙、丙各自击中目标的概率;(2)求目标被击中的概率.
17
解:(1)记甲、乙、丙各自独立击中目标的事件分别为A、B、C.
则由已知,得P(A)=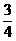 ,P(
,P( ·
·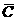 )=P(
)=P( )P(
)P(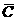 )=
)=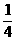 [1-P(C)]=
[1-P(C)]=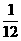 ,∴P(C)=
,∴P(C)=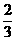 ………3分
………3分
由P(B·C)=P(B)P(C)=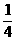 ,得
,得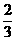 P(B)=
P(B)=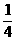 ,∴P(B)=
,∴P(B)=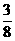 . …………8分
. …………8分
(2)目标被击中的概率为
1-P( ·
·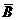 ·
·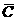 )=1-[1-P(A)][1-P(B)][1-P(C)]=1-(1-
)=1-[1-P(A)][1-P(B)][1-P(C)]=1-(1-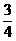 )(1-
)(1-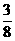 )(1-
)(1-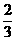 )=
)=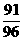 ,………10分
,………10分
答:(1)乙、丙各自击中目标概率分别为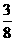 ,
,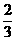 ;(2)目标被击中的概率为
;(2)目标被击中的概率为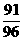 .………12分
.………12分
17. 解:(1)设事件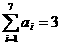 为A,则在7次抛骰子中出现5次奇数,2次偶数,
为A,则在7次抛骰子中出现5次奇数,2次偶数,
而抛骰子出现的奇数和偶数的概率为P是相等的,且为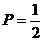
根据独立重复试验概率公式: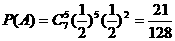 ………………………………6分
………………………………6分
(2)若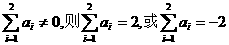 ,即前2次抛骰子中都是奇数或都是偶数.
,即前2次抛骰子中都是奇数或都是偶数.
若前2次都是奇数,则必须在后5次中抛出3次奇数2次偶数,
其概率: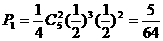 …………………………………………………………8分
…………………………………………………………8分
若前2次都是偶数,则必须在后5次中抛出5次奇数,其概率:
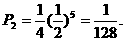 …………………………………………………………………………10分
…………………………………………………………………………10分
 所求事件的概率
所求事件的概率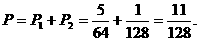 ………………………………12分
………………………………12分
17.(本小题满分12分)
抛一枚均匀的骰子(骰子的六面分别有数字1、2、3、4、5、6)来构造数列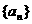 ,使
,使
 ,记
,记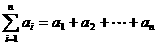 .
.
(1)求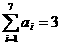 的概率;
的概率;
(2)若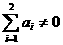 ,求
,求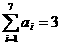 的概率.
的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com