
题目列表(包括答案和解析)
4. 在2004年雅典奥运会中,中国女排与俄罗斯女排以“五局三胜”制进行决赛,根据以往战况,中国女排在每一局赢的概率为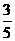 , 已知比赛中,俄罗斯女排先胜了每一局,求:
, 已知比赛中,俄罗斯女排先胜了每一局,求:
(1)中国女排在这种情况下取胜的概率;
(2)设比赛局数为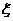 ,求
,求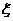 的分布列及E
的分布列及E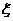 .(均用分数作答)
.(均用分数作答)
答案:(1)中国女排取胜的情况有两种,第一种是中国女排连胜三局,第二种是在第2局到第4局, 中国女排赢了两局,第5局中国女排赢,
∴中国女排取胜的概率为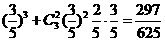
(2)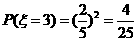 ,
,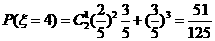
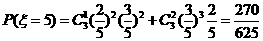 ,所以
,所以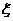 的分布列为
的分布列为
|
ξ |
3 |
4 |
5 |
|
P |
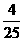 |
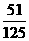 |
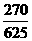 |
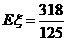 .
.
3. 某人有5把钥匙,一把是房门钥匙,但忘记了开房门的是哪一把.于是,他逐把不重复地试开,问:
(1)恰好第三次打开房门锁的概率是多少?
(2)三次内打开的概率是多少?
(3)如果5把内有2把房门钥匙,那么三次内打开的概率是多少?
答案:5把钥匙,逐把试开有A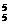 种等可能的结果.
种等可能的结果.
(1)第三次打开房门的结果有A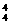 种,因此第三次打开房门的概率P(A)=
种,因此第三次打开房门的概率P(A)=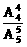 =
=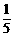 .
.
(2)三次内打开房门的结果有3A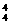 种,因此,所求概率P(A)=
种,因此,所求概率P(A)=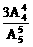 =
=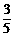 .
.
(3)方法一:因5把内有2把房门钥匙,故三次内打不开的结果有A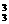 A
A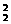 种,从而三次内打开的结果有A
种,从而三次内打开的结果有A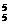 -A
-A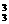 A
A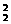 种,所求概率P(A)=
种,所求概率P(A)=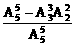 =
=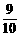 .
.
方法二:三次内打开的结果包括:三次内恰有一次打开的结果有C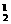 A
A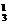 A
A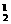 A
A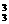 种;三次内恰有2次打开的结果有A
种;三次内恰有2次打开的结果有A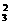 A
A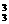 种.因此,三次内打开的结果有C
种.因此,三次内打开的结果有C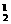 A
A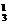 A
A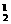 A
A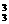 +A
+A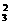 A
A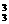 种,所求概率
种,所求概率
P(A)=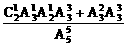 =
=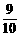 .
.
19.已知圆锥曲线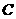 :
: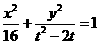 (
(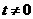 且
且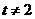 ),其两个不同的焦点
),其两个不同的焦点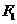 、
、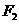 同在
同在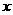 轴上.
轴上.
(1)试根据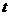 不同的取值范围来讨论
不同的取值范围来讨论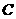 所表示的圆锥曲线;
所表示的圆锥曲线;
(2)试在曲线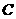 上求满足
上求满足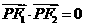 的点
的点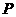 的个数,并求出相应的
的个数,并求出相应的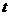 的取值范围.
的取值范围.
18.已知平面上三个向量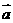 ,
,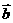 ,
,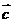 的模均为1,它们相互之间的夹角均为
的模均为1,它们相互之间的夹角均为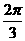 .
.
(1)求证: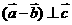 ;
;
(2)若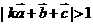 (
( ),求
),求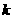 的取值范围.
的取值范围.
17.定义:在直角坐标系中,若不在一直线上的三点 、
、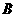 、
、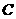 的坐标分别为
的坐标分别为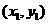 、
、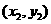 、
、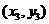 ,则三角形
,则三角形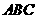 的面积可以表示为
的面积可以表示为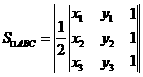 .
.
已知抛物线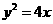 ,过抛物线焦点
,过抛物线焦点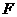 斜率为
斜率为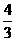 的直线
的直线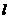 与抛物线交于
与抛物线交于 、
、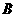 两点.
两点.
(1)求 、
、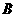 两点的坐标;
两点的坐标;
(2)若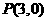 ,试用行列式计算三角形面积的方法求四边形
,试用行列式计算三角形面积的方法求四边形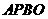 的面积
的面积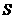 .
.
16.设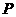 是圆
是圆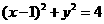 上任意一点,过
上任意一点,过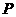 作
作 轴,
轴,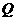 为垂足,求线段
为垂足,求线段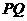 的中点
的中点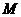 的轨迹方程,并画出图形.
的轨迹方程,并画出图形.
题10分)
15.已知直线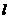 :
: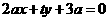 (
(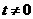 ,
, )经过点
)经过点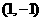 ,求直线
,求直线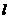 的倾斜角
的倾斜角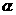 (结果精确到
(结果精确到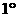 )
)
14.设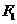 、
、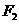 是双曲线
是双曲线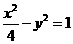 的两个焦点,点
的两个焦点,点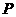 在双曲线上,且
在双曲线上,且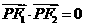 ,则
,则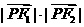 的值等于
( )
的值等于
( )
(A)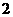 (B)
(B)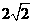 (C)
(C)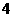 (D)
(D)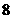
13.若直线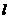 是圆
是圆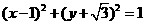 的一个切线方程,则直线
的一个切线方程,则直线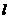 的方程可以是 ( )
的方程可以是 ( )
(A)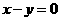 (B)
(B)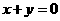 (C)
(C)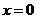 (D)
(D)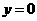
12.若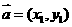 ,
,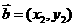 都是非零向量,且
都是非零向量,且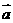 与
与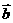 垂直,则下列行列式的值为零的是
( )
垂直,则下列行列式的值为零的是
( )
(A)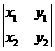 (B)
(B)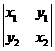 (C)
(C)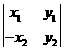 (D)
(D)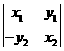
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com