
题目列表(包括答案和解析)
5、设|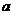 |<1,|
|<1,|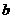 |<1,则
|<1,则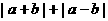 与2的大小关系是____________.
与2的大小关系是____________.
4、设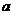 、b、c
、b、c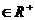 ,则三个数
,则三个数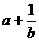 ,
,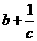 ,
,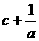 的值至少有一个不__________2(填“>”或“<”).
的值至少有一个不__________2(填“>”或“<”).
3、设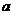 是三个互异正数
是三个互异正数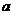 、b、c中的最大数,且
、b、c中的最大数,且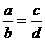 ,则
,则 (填“>”或“<”).
(填“>”或“<”).
2、设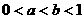 ,下列不等式中正确的是
( )
,下列不等式中正确的是
( )
A.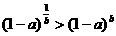 B.
B.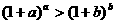
C.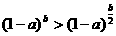 D.
D.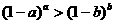
1、设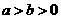 ,则下列各式中成立的是
( )
,则下列各式中成立的是
( )
A.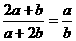 B.
B.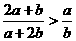
C. 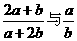 大小不定 D.
大小不定 D.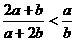
4、若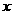 、
、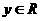 ,且
,且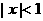 ,则
,则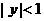 是
是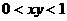 的___________条件.
的___________条件.
例题选讲
例1、已知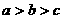 ,且
,且 =0,求证:
=0,求证: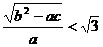 .
.
例2、设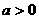 ,求证:
,求证: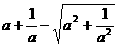 ≤
≤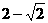 .
.
例3、设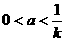 ,
,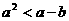 ,求证:
,求证: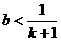 (
(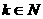 ,
,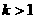 ).
).
例4、用反证法证明:
(1)若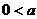 、
、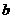 、
、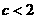 ,求证:
,求证: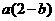 、
、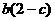 、
、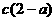 不可能都大于1.
不可能都大于1.
(2)已知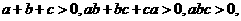 求证:
求证: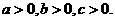
课后练习
班级_______学号__________姓名_________
3、设正数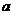 、b、c满足
、b、c满足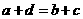 且
且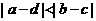 ,则 ( )
,则 ( )
A.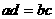 B.
B.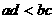
C.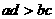 D.
D.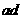 与
与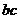 大小不定
大小不定
2、设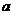 、b、c不全为O,且
、b、c不全为O,且 =0,则
(
)
=0,则
(
)
A.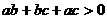 B.
B.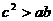
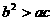
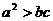
C.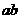 、
、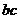 、
、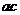 均为负数 D.
均为负数 D.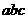 <0
<0
1、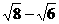 与
与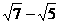 的大小关系是______________.
的大小关系是______________.
2、反证法:据“正难则反”原则,解决结论是“至少有一个”、“至多有一个”、“都大于”等类型的问题。其证明的一般步骤是:反设结论 → 逻辑推理 → 导出矛盾 → 肯定结论.
重点难点
重点:用分析法证明简单的不等式.
难点:反证法证明简单不等式过程中矛盾的导出.
基础训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com