
题目列表(包括答案和解析)
1.(如中)已知向量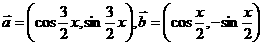 ,且
,且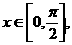 求
求
(1) 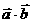 及
及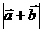 ;
;
(2)若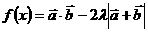 的最小值是
的最小值是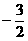 ,求实数
,求实数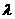 的值.
的值.
错误分析:(1)求出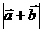 =
=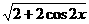 后,而不知进一步化为
后,而不知进一步化为 ,人为增加难度;
,人为增加难度;
(2)化为关于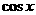 的二次函数在
的二次函数在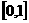 的最值问题,不知对对称轴方程讨论.
的最值问题,不知对对称轴方程讨论.
答案: (1)易求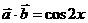 ,
, 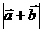 =
= ;
;
(2)
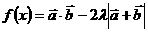 =
=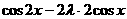 =
=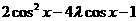
=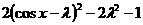
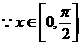
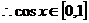
从而:当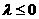 时,
时,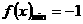
 与题意矛盾,
与题意矛盾,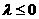 不合题意;
不合题意;
当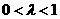 时,
时,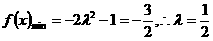 ;
;
当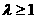 时,
时,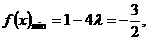 解得
解得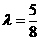 ,不满足
,不满足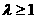 ;
;
综合可得: 实数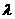 的值为
的值为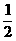 .
.
5.(案中)已知o为坐标原点,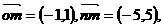 集合
集合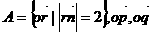
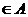 ,且
,且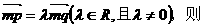
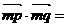 。
。
正确答案:46
错误原因:看不懂题意,未曾想到数形结合的思想。
4.(案中)若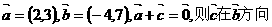 上的投影为
。
上的投影为
。
正确答案: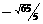
错误原因:投影的概念不清楚。
3.(薛中)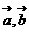 是任意向量,给出:1
是任意向量,给出:1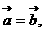 2
2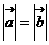 ,3
,3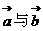 方向相反,4
方向相反,4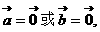 5
5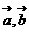 都是单位向量,其中
是
都是单位向量,其中
是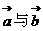 共线的充分不必要条件。
共线的充分不必要条件。
答案:134
错解:13
错因:忽略 方向的任意性,从而漏选。
方向的任意性,从而漏选。
1、(薛中)设平面向量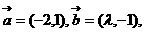 若
若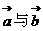 的夹角是钝角,则
的夹角是钝角,则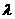 的范围是
。
的范围是
。
答案: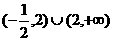
错解: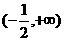

错因:“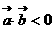 ”与“
”与“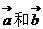 的夹角为钝角”不是充要条件。
的夹角为钝角”不是充要条件。
2.(一中)有两个向量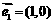 ,
,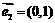 ,今有动点
,今有动点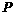 ,从
,从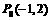 开始沿着与向量
开始沿着与向量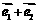 相同的方向作匀速直线运动,速度为
相同的方向作匀速直线运动,速度为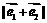 ;另一动点
;另一动点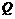 ,从
,从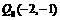 开始沿着与向量
开始沿着与向量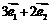 相同的方向作匀速直线运动,速度为
相同的方向作匀速直线运动,速度为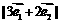 .设
.设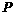 、
、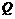 在时刻
在时刻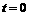 秒时分别在
秒时分别在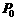 、
、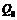 处,则当
处,则当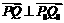 时,
时,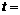 秒.正确答案:2
秒.正确答案:2
1.(如中)若向量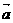 =
=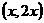 ,
,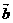 =
=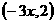 ,且
,且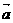 ,
,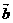 的夹角为钝角,则
的夹角为钝角,则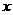 的取值范围是______________.
的取值范围是______________.
错误分析:只由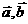 的夹角为钝角得到
的夹角为钝角得到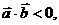 而忽视了
而忽视了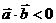 不是
不是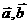 夹角为钝角的充要条件,因为
夹角为钝角的充要条件,因为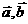 的夹角为
的夹角为 时也有
时也有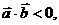 从而扩大
从而扩大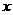 的范围,导致错误.
的范围,导致错误.
正确解法:
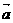 ,
,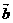 的夹角为钝角,
的夹角为钝角, 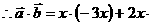
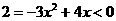
解得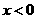 或
或 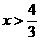
 (1)
(1)
又由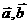 共线且反向可得
共线且反向可得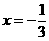 (2)
(2)
由(1),(2)得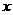 的范围是
的范围是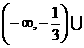
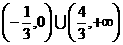
答案: 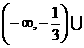
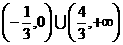 .
.
29.(案中)设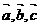 是任意的非零平面向量且互不共线,以下四个命题:
是任意的非零平面向量且互不共线,以下四个命题:
①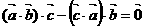 ②
②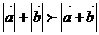
③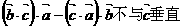 ④若
④若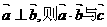 不平行
不平行
其中正确命题的个数是
( )
A、1个 B、2个 C、3个 D、4个
正确答案:(B)
错误原因:本题所述问题不能全部搞清。
二填空题:
28.(案中)已知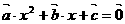 是关于x的一元二次方程,其中
是关于x的一元二次方程,其中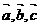 是非零向量,且向量
是非零向量,且向量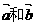 不共线,则该方程
( )
不共线,则该方程
( )
A、至少有一根 B、至多有一根
C、有两个不等的根 D、有无数个互不相同的根
正确答案:(B)
错误原因:找不到解题思路。
27.(案中)已知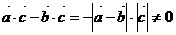 ,且
,且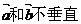 ,则
,则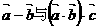 ( )
( )
A、相等 B、方向相同 C、方向相反 D、方向相同或相反
正确答案:(D)
错误原因:受已知条件的影响,不去认真思考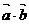 可正可负,易选成B。
可正可负,易选成B。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com