
题目列表(包括答案和解析)
7、辅助角公式中辅助角的确定:
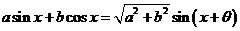 (其中
(其中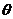 角所在的象限由a, b的符号确定,
角所在的象限由a, b的符号确定,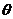 角的值由
角的值由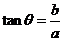 确定)在求最值、化简时起着重要作用。
确定)在求最值、化简时起着重要作用。
6.三角函数的恒等变形的基本思路是:一角二名三结构。即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心!第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点。基本的技巧有:
(1)巧变角如(2)三角函数名互化(切割化弦),
(3)公式变形使用(4)三角函数次数的降升,
(5)式子结构转化(对角、函数名、式子结构化同)。
(6)常值变换主要指“1”的变换
(7)正余弦“三兄妹-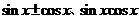 ”的内存联系――“知一求二”,
”的内存联系――“知一求二”,
5.特殊角的三角函数值:
4.三角函数线的特征是:正弦线MP“站在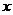 轴上(起点在
轴上(起点在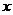 轴上)”、余弦线OM“躺在
轴上)”、余弦线OM“躺在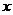 轴上(起点是原点)”、正切线AT“站在点
轴上(起点是原点)”、正切线AT“站在点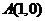 处(起点是
处(起点是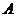 )”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。
)”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。
3、任意角的三角函数的定义:设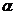 是任意一个角,P
是任意一个角,P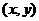 是
是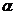 的终边上的任意一点(异于原点),
的终边上的任意一点(异于原点),
它与原点的距离是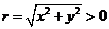 ,那么
,那么
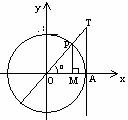
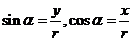 ,
,
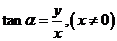 ,
,
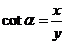
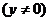
2.弧长公式: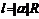 ,扇形面积公式:
,扇形面积公式:
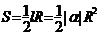 ,1弧度(1rad)
,1弧度(1rad)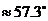 .
.
10.面积定理
(1)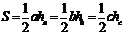 (
(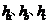 分别表示a、b、c边上的高).
分别表示a、b、c边上的高).
三基本概念
1象限角的概念:如果角的终边在坐标轴上,就认为这个角不属于任何象限。
8.正弦定理
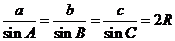 .9.余弦定理
.9.余弦定理
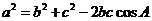 ;
;
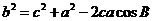 ;
;
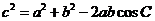 .
.
7.三角函数的周期公式
函数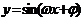 ,x∈R及函数
,x∈R及函数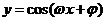 ,x∈R(A,ω,
,x∈R(A,ω,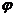 为常数,且A≠0,ω>0)的周期
为常数,且A≠0,ω>0)的周期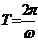 ;函数
;函数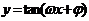 ,
,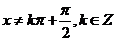 (A,ω,
(A,ω,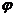 为常数,且A≠0,ω>0)的周期
为常数,且A≠0,ω>0)的周期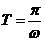 .
.
|
性质 |
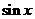 |
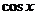 |
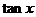 |
|
图像的来源 及图像 |
|
|
|
|
定义域 |
|
|
|
|
值域 |
|
|
|
|
单调性及 递增递减区间 |
|
|
|
|
周期性及 奇偶性 |
|
|
|
|
对称轴 |
|
|
|
|
对称中心 |
|
|
|
|
最值及指定区间的最值 |
|
|
|
|
简单三角方程和不等式 |
|
|
|
|
|
30° |
45° |
60° |
0° |
90° |
180° |
270° |
15° |
75° |
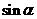 |
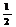 |
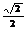 |
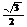 |
0 |
1 |
0 |
-1 |
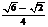 |
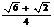 |
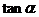 |
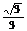 |
1 |
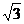 |
0 |
|
0 |
|
2-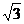 |
2+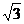 |
5.二倍角公式
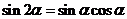 .
.
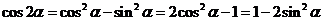
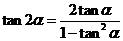 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com