
题目列表(包括答案和解析)
11、某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙投资的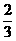 倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确规划投资后,在这两个项目上共可获得的最大利润为( )
倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确规划投资后,在这两个项目上共可获得的最大利润为( )
(A)36万元 (B)31.2万元 (C)30.4万元 (D)24万元
解析:选B.对甲项目投资24万元,对乙项目投资36万元,可获最大利润31.2万元.因为对乙项目投资获利较大,故在投资规划要求内(对项目甲的投资不小于对项目乙投资的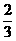 倍)尽可能多地安排资金投资于乙项目,即对项目甲的投资等于对项目乙投资的
倍)尽可能多地安排资金投资于乙项目,即对项目甲的投资等于对项目乙投资的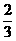 倍时可获最大利润.这是最优解法.也可用线性规划的通法求解.注意线性规划在高考中以应用题型的形式出现.
倍时可获最大利润.这是最优解法.也可用线性规划的通法求解.注意线性规划在高考中以应用题型的形式出现.
10、已知抛物线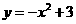 上存在关于直线
上存在关于直线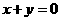 对称的相异两点
对称的相异两点 、
、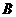 ,则
,则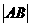 等于( )
等于( )
(A)3
(B)4
(C)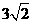 (D)
(D)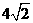
解析:选C.设直线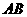 的方程为
的方程为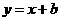 ,由
,由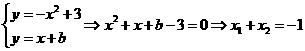 ,进而可求出
,进而可求出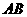 的中点
的中点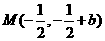 ,又由
,又由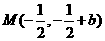 在直线
在直线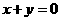 上可求出
上可求出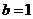 ,∴
,∴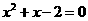 ,由弦长公式可求出
,由弦长公式可求出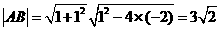 .本题考查直线与圆锥曲线的位置关系.自本题起运算量增大.
.本题考查直线与圆锥曲线的位置关系.自本题起运算量增大.
9、用数字1,2,3,4,5可以组成没有重复数字,并且比20000大的五位偶数共有( )
(A)48个 (B)36个 (C)24个 (D)18个
解析:选B.个位是2的有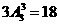 个,个位是4的有
个,个位是4的有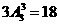 个,所以共有36个.
个,所以共有36个.
8、设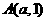 ,
,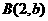 ,
,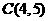 为坐标平面上三点,
为坐标平面上三点, 为坐标原点,若
为坐标原点,若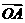 与
与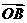 在
在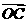 方向上的投影相同,则
方向上的投影相同,则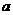 与
与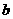 满足的关系式为( )
满足的关系式为( )
(A)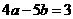 (B)
(B)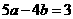 (C)
(C)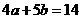 (D)
(D)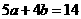
解析:选A.由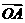 与
与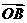 在
在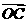 方向上的投影相同,可得:
方向上的投影相同,可得: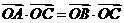 即
即 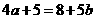 ,
,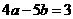 .
.
7、等差数列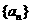 中,
中,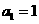 ,
,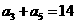 ,其前
,其前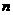 项和
项和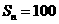 ,则
,则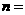 ( )
( )
(A)9 (B)10 (C)11 (D)12
解析:选B.
6、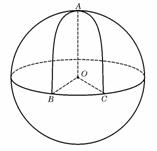 设球
设球 的半径是1,
的半径是1, 、
、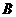 、
、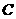 是球面上三点,已知
是球面上三点,已知 到
到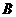 、
、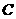 两点的球面距离都是
两点的球面距离都是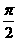 ,且二面角
,且二面角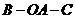 的大小是
的大小是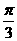 ,则从
,则从 点沿球面经
点沿球面经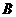 、
、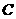 两点再回到
两点再回到 点的最短距离是( )
点的最短距离是( )
(A)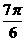 (B)
(B)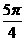
(C)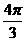 (D)
(D)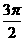
解析:选C.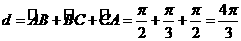 .本题考查球面距离.
.本题考查球面距离.
5、如果双曲线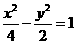 上一点
上一点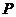 到双曲线右焦点的距离是2,那么点
到双曲线右焦点的距离是2,那么点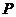 到
到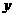 轴的距离是( )
轴的距离是( )
(A)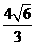 (B)
(B)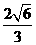 (C)
(C)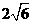 (D)
(D)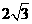
解析:选A.由点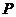 到双曲线右焦点
到双曲线右焦点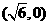 的距离是2知
的距离是2知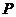 在双曲线右支上.又由双曲线的第二定义知点
在双曲线右支上.又由双曲线的第二定义知点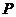 到双曲线右准线的距离是
到双曲线右准线的距离是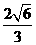 ,双曲线的右准线方程是
,双曲线的右准线方程是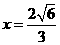 ,故点
,故点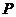 到
到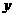 轴的距离是
轴的距离是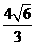 .
.
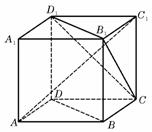
4、如图,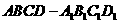 为正方体,下面结论错误的是( )
为正方体,下面结论错误的是( )
(A)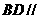 平面
平面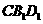
(B)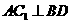
(C)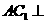 平面
平面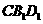
(D)异面直线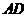 与
与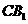 所成的角为60°
所成的角为60°
解析:选D.
3、某商场买来一车苹果,从中随机抽取了10个苹果,其重量(单位:克)分别为:150,152,153,149,148,146,151,150,152,147,由此估计这车苹果单个重量的期望值是( )
 (A)150.2克 (B)149.8克 (C)149.4克 (D)147.8克
(A)150.2克 (B)149.8克 (C)149.4克 (D)147.8克
解析:选B.
2、函数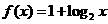 与
与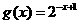 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )
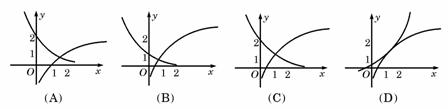
解析:选C.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com