
题目列表(包括答案和解析)
6.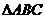 中,
中,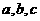 分别为角A,B,C的对边,若
分别为角A,B,C的对边,若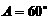 ,
,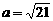 ,
,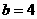 ,则边
,则边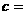 .
.
5.若圆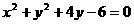 关于直线
关于直线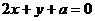 对称,则实数
对称,则实数 的值为_______.
的值为_______.
4.向量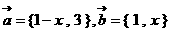 ,若
,若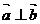 ,则实数
,则实数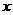 =_______.
=_______.
3.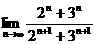 =___________.
=___________.
2.等差数列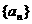 中,
中,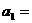 4,
4,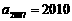 ,则公差
,则公差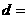 .
.
1.设集合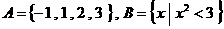 ,则A∩B =___________________.
,则A∩B =___________________.
22.(本题满分18分.第(1)题4分,第(2)题14分,分别为4、4、6分)
已知抛物线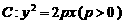 上横坐标为
上横坐标为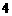 的点到焦点的距离为
的点到焦点的距离为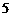 .
.
(1)求抛物线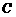 的方程.
的方程.
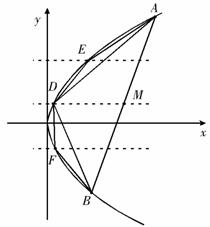
(2)设直线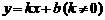 与抛物线
与抛物线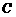 交于两点
交于两点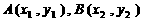 ,且
,且
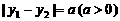 ,
,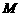 是弦
是弦 的中点,过
的中点,过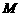 作平行于
作平行于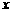 轴的直线交抛物线
轴的直线交抛物线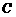 于点
于点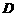 ,得到
,得到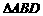 ;再分别过弦
;再分别过弦 、
、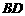 的中点作平行于
的中点作平行于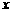 轴的直线依次交抛物线
轴的直线依次交抛物线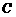 于点
于点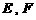 ,得到
,得到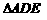 和
和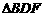 ;按此方法继续下去.
;按此方法继续下去.
解决下列问题:
1 求证: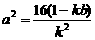 ;
;
2 计算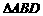 的面积
的面积 ;
;
3 根据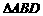 的面积
的面积 的计算结果,写出
的计算结果,写出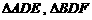
的面积;请设计一种求抛物线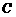 与线段
与线段 所围成封闭图
所围成封闭图
形面积的方法,并求出此封闭图形的面积.
[解]
上海市浦东新区2007年高考预测
21.(本题满分16分,第(1)题4分,第(2)题7分,第(3)题5分)
记函数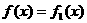 ,
,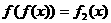 ,它们定义域的交集为
,它们定义域的交集为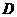 ,若对任意的
,若对任意的
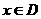 ,
,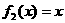 ,则称
,则称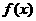 是集合
是集合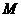 的元素.
的元素.
(1)判断函数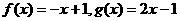 是否是
是否是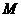 的元素;
的元素;
(2)设函数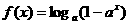 ,求
,求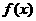 的反函数
的反函数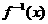 ,并判断
,并判断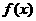 是否是
是否是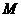 的元素;
的元素;
(3)若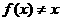 ,写出
,写出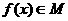 的条件,并写出两个不同于(1)、(2)中的函数.(将根据写出的函数类型酌情给分)
的条件,并写出两个不同于(1)、(2)中的函数.(将根据写出的函数类型酌情给分)
[解]
20.(本题满分14分,第(1)题7分,第(2)题7分)
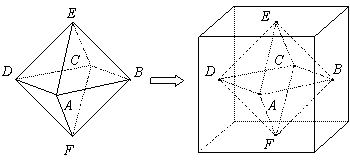
两个相同的正四棱锥底面重合组成一个八面体,可放于棱长为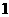 的正方体中,重合的底面与正方体的某一个面平行,各顶点均在正方体的表面上,把满足上述条件的八面体称为正方体的“正子体”.
的正方体中,重合的底面与正方体的某一个面平行,各顶点均在正方体的表面上,把满足上述条件的八面体称为正方体的“正子体”.
(1)若正子体的六个顶点分别是正方体各面的中心,求异面直线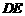 与
与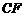 所成的角;
所成的角;
(2)问此正子体的体积V是否为定值?若是,求出该定值;若不是,求出体积大小的取值范围.
[解]
19.(本题满分14分,第(1)题6分,第(2)题8分)
等差数列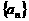 中,前
中,前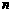 项和为
项和为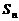 ,首项
,首项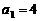 ,
,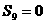 .
.
(1)若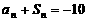 ,求
,求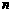 ;
;
(2)设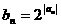 ,求使不等式b1 + b2 + … + bn >
2007的最小正整数
,求使不等式b1 + b2 + … + bn >
2007的最小正整数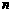 的值.
的值.
[解]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com