
题目列表(包括答案和解析)
19. (14分)对1个单位质量的含污物体进行清洗,
清洗前其清洁度(含污物体的清洁度定义为: 为
为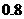 , 要求清洗完后的清洁度为
, 要求清洗完后的清洁度为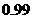 . 有两种方案可供选择, 方案甲:
一次清洗;
方案乙: 分两次清洗. 该物体初次清洗后受残留水等因素影响, 其质量变为
. 有两种方案可供选择, 方案甲:
一次清洗;
方案乙: 分两次清洗. 该物体初次清洗后受残留水等因素影响, 其质量变为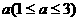 . 设用
. 设用 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是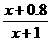
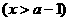 , 用
, 用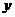 单位质量的水第二次清洗后的清洁度是
单位质量的水第二次清洗后的清洁度是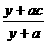 , 其中
, 其中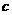
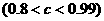 是该物体初次清洗后的清洁度.
是该物体初次清洗后的清洁度.
(1)分别求出方案甲以及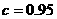 时方案乙的用水量, 并比较哪一种方案用水量较少;
时方案乙的用水量, 并比较哪一种方案用水量较少;
(2)若采用方案乙, 当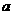 为某固定值时, 如何安排初次与第二次清洗的用水量, 使总用水量最小? 并讨论
为某固定值时, 如何安排初次与第二次清洗的用水量, 使总用水量最小? 并讨论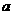 取不同数值时对最少总用水量多少的影响.
取不同数值时对最少总用水量多少的影响.
18. (14分)已知集合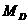 是满足下列性质函数
是满足下列性质函数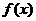 的全体:若函数
的全体:若函数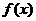 的定义域为D,对于任意的
的定义域为D,对于任意的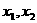
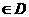 (
(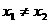 ),有
),有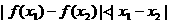 。
。
(I)当D=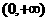 时,
时,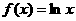 是否属于
是否属于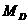 ,若属于
,若属于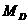 ,给予证明。否则说明理由;
,给予证明。否则说明理由;
(II)当D= 时,函数
时,函数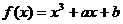 时,若
时,若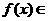
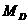 ,求实数a的取值范围。
,求实数a的取值范围。
17. (14分)已知函数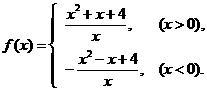
(1)求证:函数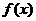 是偶函数;
是偶函数;
(2)判断函数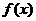 分别在区间
分别在区间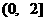 、
、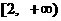 上的单调性, 并加以证明;
上的单调性, 并加以证明;
(3)若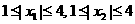 , 求证:
, 求证:  .
.
16. (12分) ) 已知函数 在点
在点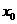 处取得极大值
处取得极大值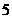 ,其导函数
,其导函数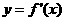 的图象经过点
的图象经过点 ,
,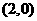 ,如图所示.求:
,如图所示.求:
(Ⅰ)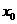 的值;(Ⅱ)
的值;(Ⅱ)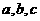 的值.
的值.
15. (12分)设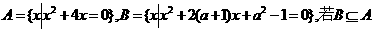 ,求实数
,求实数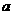 的取值范围。
的取值范围。
14. 设函数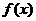 的定义域为R,若存在常数m>0,使
的定义域为R,若存在常数m>0,使 对一切实数x均成立,则称
对一切实数x均成立,则称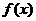 为F函数.给出下列函数:
为F函数.给出下列函数:
①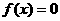 ;②
;②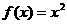 ;③
;③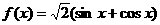 ;④
;④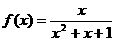 ;
;
⑤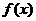 是定义在R上的奇函数,且满足对一切实数x1、x2均有
是定义在R上的奇函数,且满足对一切实数x1、x2均有 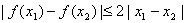 .其中是F函数的序号为_____________________.
.其中是F函数的序号为_____________________.
13. 曲线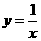 和
和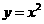 在它们交点处的两条切线与
在它们交点处的两条切线与 轴所围成的三角形面积是
.
轴所围成的三角形面积是
.
12. 函数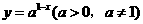 的图象恒过定点
的图象恒过定点 ,若点
,若点 在直线
在直线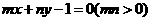 上,则
上,则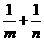 的最小值为
.
的最小值为
.
11. 若函数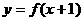 的定义域是
的定义域是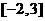 ,则
,则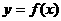 的定义域为
;
的定义域为
; 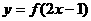 的定义域为
.
的定义域为
.
10. 函数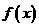 对于任意实数
对于任意实数 满足条件
满足条件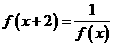 ,若
,若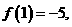 则
则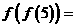 __________.
__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com