
题目列表(包括答案和解析)
4、已知关于x的方程sin2x+2cosx+a=0有解,则a的取值范围是__________.
原方程可化为cos2x-2cosx-a-1=0,令t=cosx,得t2-2t-a-1=0,原问题转化为方程t2-2t-a-1=0在[-1,1]上至少有一个实根.令f(t)=t2-2t-a-1,对称轴t=1,画图象分析可得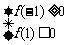 解得a∈[-2,2].答案:[-2,2]
解得a∈[-2,2].答案:[-2,2]
3、已知f(x)、g(x)都是奇函数,f(x)>0的解集是(a2,b),g(x)>0的解集是(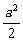 ,
,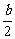 ),
),
则f(x)·g(x)>0的解集是__________.
解析:由已知b>a2∵f(x),g(x)均为奇函数,∴f(x)<0的解集是(-b,-a2),g(x)<0的解集是(-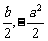 ).由f(x)·g(x)>0可得:
).由f(x)·g(x)>0可得:
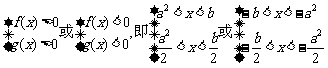
∴x∈(a2,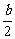 )∪(-
)∪(-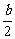 ,-a2)答案:(a2,
,-a2)答案:(a2,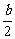 )∪(-
)∪(-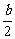 ,-a2)
,-a2)
2、设正数a、b、c、d满足a+d=b+c,且|a-d|<|b-c|,则ad与bc的大小关系是__________.
解析:由0≤|a-d|<|b-c|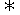 (a-d)2<(b-c)2
(a-d)2<(b-c)2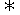 (a+b)2-4ad<(b+c)2-4bc?
(a+b)2-4ad<(b+c)2-4bc?
∵a+d=b+c,∴-4ad<-4bc,故ad>bc.答案:ad>bc
1、已知x、y是正变数,a、b是正常数,且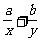 =1,x+y的最小值为__________.
=1,x+y的最小值为__________.
解析:令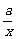 =cos2θ,
=cos2θ,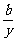 =sin2θ,则x=asec2θ,y=bcsc2θ,∴x+y=asec2θ+bcsc2θ=a+b+atan2θ+bcot2θ≥a+b+2
=sin2θ,则x=asec2θ,y=bcsc2θ,∴x+y=asec2θ+bcsc2θ=a+b+atan2θ+bcot2θ≥a+b+2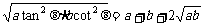 .答案:a+b+2
.答案:a+b+2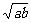
11.(1)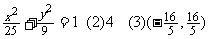
10. (1)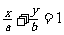 (3)90o
(3)90o
9.(1)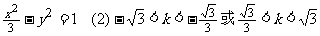
6. 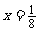 7.
7.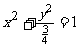 8. y2=4x或y2= -36x
8. y2=4x或y2= -36x
11.已知椭圆的焦点是F1(-4,0)、F2(4,0),过F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10,椭圆上的不同两点A(x1,y1)、C (x2,y2)满足条件|F2A|、
|F2B|、|F2C|、成等差数列。
(1)求椭圆的方程; (2)求弦AC中点的横坐标;
(3)设弦AC的垂直平分线的方程为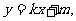 求m的取值范围。
求m的取值范围。
答案: 1.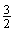 2. 90o 3. 5
4.
2. 90o 3. 5
4.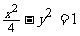 5.
5. 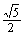
10. 如图,O为坐标原点,直线
如图,O为坐标原点,直线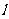 在
在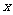 轴和
轴和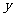 轴上的截距分别是
轴上的截距分别是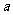 和
和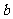 ,且交抛物线
,且交抛物线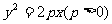 于
于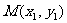 、
、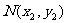 两点。
两点。
(1)写出直线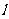 的截距式方程; (2)证明:
的截距式方程; (2)证明: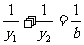 ;
;
(3)当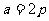 时,求
时,求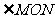 的大小。
的大小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com