
题目列表(包括答案和解析)
18.设函数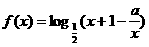 在区间
在区间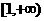 上单调递减,求实数a的取值范围.
上单调递减,求实数a的取值范围.
17. 通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设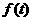 表示学生注意力随时间
表示学生注意力随时间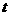 (分钟)的变化规律(
(分钟)的变化规律(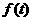 越大,表明学生注意力越集中),经过实验分析得知:
越大,表明学生注意力越集中),经过实验分析得知:
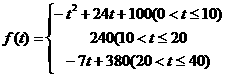
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
16、已知函数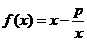 (x>1)
(x>1)
(1)若函数在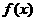 上是增函数,求实数
上是增函数,求实数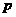 的取值范围;
的取值范围;
(2)解关于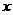 的不等式
的不等式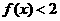 .
.
15.判断函数f(x)=(x-1)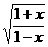 的奇偶性为____________________
的奇偶性为____________________
14、若函数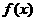 满足:对于任意
满足:对于任意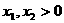 ,都有
,都有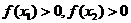 ,且
,且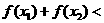
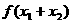 成立,则称函数
成立,则称函数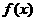 具有性质M。给出下列四个函数:①
具有性质M。给出下列四个函数:①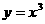 ,
,
②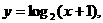 ③
③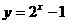 ,④
,④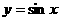 .其中具有性质M的函数是
.(注:把满足题意的所有函数的序号都填上)
.其中具有性质M的函数是
.(注:把满足题意的所有函数的序号都填上)
14、已知 的不等实根一共有 个
的不等实根一共有 个
13、函数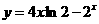 的单调递增区间是
的单调递增区间是
A.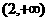 B.
B.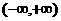 C.
C.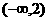 D.
D.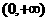
12、若函数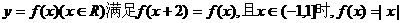 ,则函数
,则函数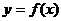 的图象与函数
的图象与函数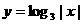 的图象的交点个数为:
的图象的交点个数为:
A.2 B.3 C.4 D.无数个
11、设函数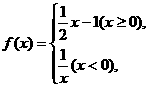 若
若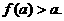 则实数
则实数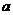 的取值范围是
.
的取值范围是
.
10、已知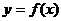 是偶函数,当
是偶函数,当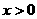 时,
时,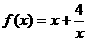 ,且当
,且当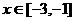 时,
时,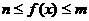
恒成立,则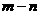 的最小值是:
的最小值是:
A.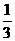 B.
B.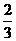 C.1 D.
C.1 D.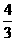
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com