
题目列表(包括答案和解析)
14.二次方程、二次不等式、二次函数间的联系你了解了吗?二次方程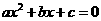 的两个根即为二次不等式
的两个根即为二次不等式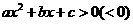 的解集的端点值,也是二次函数
的解集的端点值,也是二次函数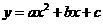 的图象与
的图象与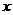 轴的交点的横坐标。8.
9.(1)(答:①④);(2)(答:
轴的交点的横坐标。8.
9.(1)(答:①④);(2)(答: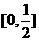 )(3)B.(4) B.( 5)B(6) B (7) A. 10.(答:
)(3)B.(4) B.( 5)B(6) B (7) A. 10.(答: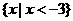 )11.(答:当
)11.(答:当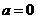 时,
时,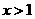 ;当
;当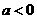 时,
时,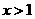 或
或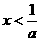 ;当
;当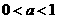 时,
时,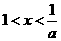 ;当
;当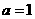 时,
时,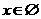 ;当
;当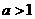 时,
时,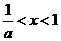 )12.(1)(答:
)12.(1)(答: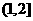 );(2)(答:
);(2)(答: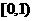 )13.(答:(
)13.(答:(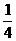 ,1)) 14.(答:
,1)) 14.(答: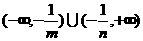 )
)
13.一元二次方程根的分布理论。方程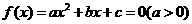 在
在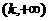 上有两根、在
上有两根、在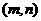 上有两根、在
上有两根、在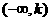 和
和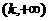 上各有一根的充要条件分别是什么?
上各有一根的充要条件分别是什么?
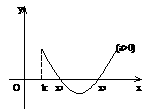 (
(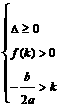 、
、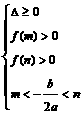 、
、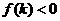 )。根的分布理论成立的前提是开区间,若在闭区间
)。根的分布理论成立的前提是开区间,若在闭区间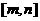 讨论方程
讨论方程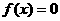 有实数解的情况,可先利用在开区间
有实数解的情况,可先利用在开区间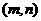 上实根分布的情况,得出结果,再令
上实根分布的情况,得出结果,再令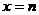 和
和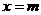 检查端点的情况.
检查端点的情况.
12. 对于方程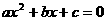 有实数解的问题。首先要讨论最高次项系数
有实数解的问题。首先要讨论最高次项系数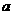 是否为0,其次若
是否为0,其次若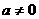 ,则一定有
,则一定有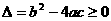 。对于多项式方程、不等式、函数的最高次项中含有参数时,你是否注意到同样的情形?
。对于多项式方程、不等式、函数的最高次项中含有参数时,你是否注意到同样的情形?
11. 一元二次不等式的解集(联系图象)。尤其当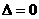 和
和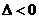 时的解集你会正确表示吗?设
时的解集你会正确表示吗?设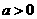 ,
,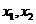 是方程
是方程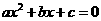 的两实根,且
的两实根,且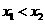 ,则其解集如下表:
,则其解集如下表:
|
|
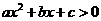 |
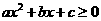 |
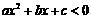 |
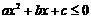 |
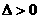 |
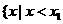 或 或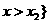 |
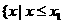 或 或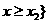 |
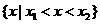 |
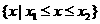 |
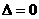 |
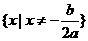 |
R |
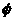 |
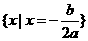 |
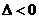 |
R |
R |
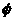 |
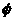 |
10. 一元一次不等式的解法:通过去分母、去括号、移项、合并同类项等步骤化为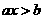 的形式,
的形式,
若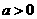 ,则
,则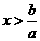 ;若
;若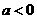 ,则
,则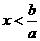 ;若
;若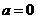 ,则当
,则当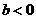 时,
时,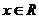 ;当
;当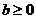 时,
时,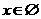 。
。
9.充要条件。
关键是分清条件和结论(划主谓宾),由条件可推出结论,条件是结论成立的充分条件;由结论可推出条件,则条件是结论成立的必要条件。从集合角度解释,若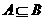 ,则A是B的充分条件;若
,则A是B的充分条件;若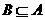 ,则A是B的必要条件;若A=B,则A是B的充要条件。
,则A是B的必要条件;若A=B,则A是B的充要条件。
14.若关于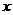 的不等式
的不等式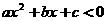 的解集为
的解集为 ,其中
,其中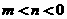 ,则关于
,则关于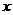 的不等式
的不等式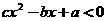 的解集为________
的解集为________
友情提示
13.实系数方程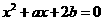 的一根大于0且小于1,另一根大于1且小于2,则
的一根大于0且小于1,另一根大于1且小于2,则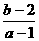 的取值范围是_________
的取值范围是_________
12.(1)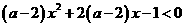 对一切
对一切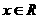 恒成立,则
恒成立,则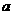 的取值范围是_______;
的取值范围是_______;
(2)关于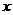 的方程
的方程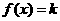 有解的条件是什么?(答:
有解的条件是什么?(答: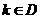 ,其中
,其中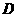 为
为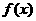 的值域),特别地,若在
的值域),特别地,若在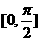 内有两个不等的实根满足等式
内有两个不等的实根满足等式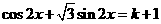 ,则实数
,则实数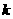 的范围是_______.
的范围是_______.
11.解关于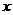 的不等式:
的不等式: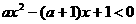 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com