
题目列表(包括答案和解析)
(15) (本小题满分14分)
已知向量 = (cos x,sin x), = (-cos x,cos x), = (-1,0)
(Ⅰ)若 x = ,求向量 、 的夹角;
(Ⅱ)当 x∈[,] 时,求函数 f (x) = 2· + 1 的最大值。
(16) (本小题满分14分)
已知函数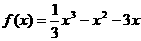 .
.
(Ⅰ) 求求函数的单调区间; (Ⅱ) 求函数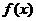 的极值
的极值
(17) (本小题满分16分)
用水清洗一堆蔬菜上残留的农药的效果假定如下:用x单位量的水清洗一次以后,蔬菜上残留的农药量与这次清洗前残留的农药量之比为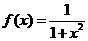 .
.
(Ⅰ)试解释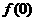 的实际意义;
的实际意义;
(Ⅱ)现有a(a>0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次.哪种方案清洗后蔬菜上残留的农药比较少?请说明理由.
(18) (本小题满分16分)
已知O为坐标原点,A(0,2),B(4,6),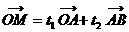 .
.
(Ⅰ) 求点M在第二或第三象限的充要条件;
(Ⅱ) 求证:当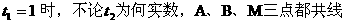 ;
;
(Ⅲ) 若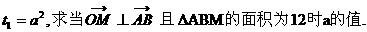
(19) (本小题满分16分)
已知函数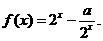 将
将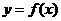 的图象向右平移两个单位,得到
的图象向右平移两个单位,得到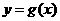 的图象.
的图象.
(Ⅰ) 求函数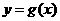 的解析式;
的解析式;
(Ⅱ) 若函数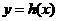 与函数
与函数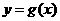 的图象关于直线
的图象关于直线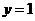 对称,求函数
对称,求函数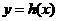 的解析式;
的解析式;
(Ⅲ) 设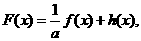 已知
已知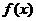 的最小值是
的最小值是 ,且
,且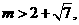 求实数
求实数
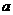 的取值范围.
的取值范围.
(20) (本小题满分16分)
设函数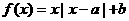
(Ⅰ) 求证: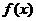 为奇函数的充要条件是
为奇函数的充要条件是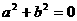 ;
;
(Ⅱ) 设常数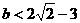 ,且对任意
,且对任意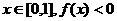 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
(1)
已知向量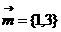 ,
,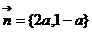 ,若
,若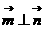 ,则
,则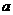 =____________.
=____________.
(2)
命题“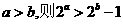 ”的否命题是____________________________________.
”的否命题是____________________________________.
(3)
若规定 的解集是____________.
的解集是____________.
(4)
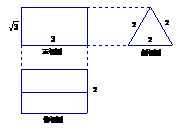
下图是一个空间几何体的三视图,根据图中尺寸(单位: ),可知几何体表面积是____________.
),可知几何体表面积是____________.
(5)
 经过点
经过点 且在两坐标轴上的截距相等的直线方程是______________________.
且在两坐标轴上的截距相等的直线方程是______________________.
(6)
双曲线的两条渐近线的夹角为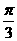 ,则双曲线的离心率是___________________.
,则双曲线的离心率是___________________.
(7)
若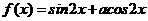 的图象关于
的图象关于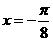 对称,则实数
对称,则实数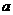 的值是__________.
的值是__________.
(8)
若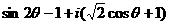 是纯虚数,则
是纯虚数,则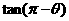 的值为____________.
的值为____________.
(9)
已知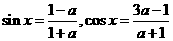 ,若
,若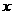 是第二象限角,则实数
是第二象限角,则实数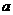 的值是____________.
的值是____________.
(10)
在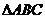 中,
中,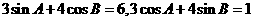 ,则
,则 等于__________.
等于__________.
(11) 设非零向量,,,若= + + ,则||的取值范围是___________.
(12)
设命题p:函数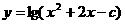 的定义域为R,命题q:函数
的定义域为R,命题q:函数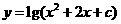 的值域为R,若命题p、q有且仅有一个正确,则c的取值范围为___________.
的值域为R,若命题p、q有且仅有一个正确,则c的取值范围为___________.
(13) 已知在平面直角坐标系中,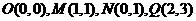 ,动点
,动点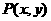 满足不等式
满足不等式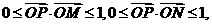 则
则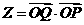 的最大值为__________.
的最大值为__________.
(14) 已知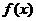 是定义在R上的偶函数,定义在R上的奇函数
是定义在R上的偶函数,定义在R上的奇函数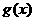 过点
过点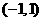 且
且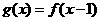 ,则
,则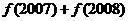 =___________.
=___________.
20、 (本小题满分14分)已知函数: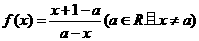
(1)当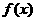 的定义域为
的定义域为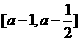 时,求函数
时,求函数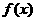 的值域;
的值域;
(2)设函数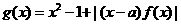 ,求函数
,求函数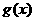 的最小值。
的最小值。
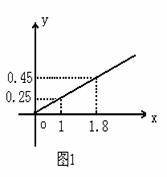
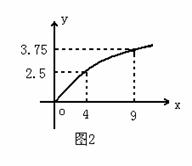
19、(本小题满分15分)某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2。(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这
10万元投资,才能使企业获得最大利润,其最大利润约为多少万元?(精确到1万元)。
18、(本小题满分15分)在等差数列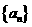 中,
中,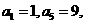 在数列
在数列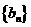 中,
中,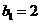 ,且
,且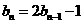 ,(n≥2)
,(n≥2)
(1)求数列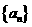 和
和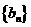 的通项公式;
的通项公式;
(2)设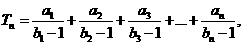 求
求 .
.
17、(本小题满分15分)
已知矩形ABCD中,AB=2AD=4,E为 CD的中点,沿AE将 AED折起,
AED折起,
 使DB=2
使DB=2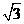 ,O、H分别为AE、AB的中点.
,O、H分别为AE、AB的中点.
(1)求证:直线OH//面BDE;
(2)求证:面ADE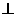 面ABCE;
面ABCE;
16、(本小题满分15分)设 点为坐标原点,曲线
点为坐标原点,曲线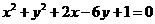 上有两点
上有两点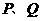 满足关于直线
满足关于直线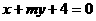 对称,又满足
对称,又满足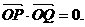
(1)求m的值;
(2)求直线PQ的方程.
15、 (本小题满分15分)已知函数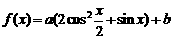
⑴ 当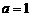 时,求
时,求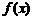 的单调递增区间;
的单调递增区间;
⑵ 当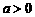 ,且
,且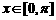 时,
时,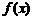 的值域是
的值域是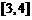 ,求
,求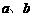 的值.
的值.
14.给出下列四个命题,其中不正确命题的序号是 .
①若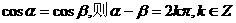 ;②函数
;②函数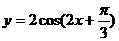 的图象关于x=
的图象关于x=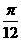 对称;③函数
对称;③函数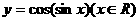 为偶函数,④函数
为偶函数,④函数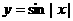 是周期函数,且周期为2
是周期函数,且周期为2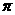 ;二、解答题(本大题共6小题,共90分. 解答应写出文字说明,证明过程或演算步骤)
;二、解答题(本大题共6小题,共90分. 解答应写出文字说明,证明过程或演算步骤)
13、设椭圆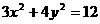 上存在两点关于直线
上存在两点关于直线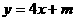 对称,则
对称,则 的取值范围是
的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com