
题目列表(包括答案和解析)
1.极限的概念和运算法则是微积分中最重要的工具,也是学好导数的基础。它是历年高考的重点考查内容,多与分类讨论相结合。通常与数列结合的题目要多一些,解答时要求先求出数列的通项公式或是前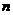 项和公式再求极限。求函数的极限时,经常要用到常见函数的极限及两个重要极限(解决函数极限的小题时可用洛毕达法则)。通过恒等变形用函数极限的四则运算法则求相关函数的极限,或利用初等函数在其定义域内每一点处的极限值等于该点函数值求函数的极限或利用函数的极限判定函数在给定点处的连续性。归纳法也是本章常见的考查点,一定要注意用数学归纳法解题时的步骤。
项和公式再求极限。求函数的极限时,经常要用到常见函数的极限及两个重要极限(解决函数极限的小题时可用洛毕达法则)。通过恒等变形用函数极限的四则运算法则求相关函数的极限,或利用初等函数在其定义域内每一点处的极限值等于该点函数值求函数的极限或利用函数的极限判定函数在给定点处的连续性。归纳法也是本章常见的考查点,一定要注意用数学归纳法解题时的步骤。
20.(14分)已知点P在曲线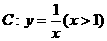 上,曲线C在点P处的切线与函数
上,曲线C在点P处的切线与函数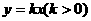 的图象交于点A,与
的图象交于点A,与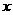 轴交于点B,设点P的横坐标为
轴交于点B,设点P的横坐标为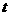 ,点A,B的横坐标分别为
,点A,B的横坐标分别为 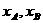 ,记
,记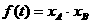
Ⅰ)求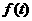 的解析式
的解析式
Ⅱ)设数列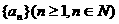 满足
满足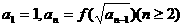 ,求数列
,求数列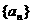 的通项公式
的通项公式
Ⅲ)在Ⅱ)的条件下,当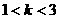 时,证明不等式
时,证明不等式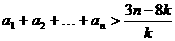
19.已知定义域为R的函数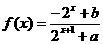 是奇函数,
是奇函数,
Ⅰ)求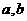 的值
的值
Ⅱ)若对任意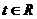 ,不等式
,不等式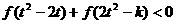 恒成立,求
恒成立,求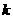 的取值范围。
的取值范围。
18.某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(Ⅰ)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(Ⅱ)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=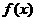 的表达式;
的表达式;
(Ⅲ)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
17.一个口袋中装有大小相同的2个白球和4个黑球.
(Ⅰ)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(Ⅱ)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的期望和方差.
16.已知向量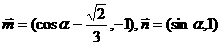 ,
, 与
与 为共线向量且
为共线向量且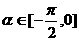
Ⅰ)求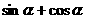 的值; Ⅱ)求
的值; Ⅱ)求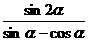 的值
的值
15.设正项等比数列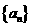 的前
的前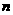 项和为
项和为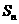 , 已知
, 已知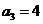 ,
,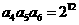 .
.
(Ⅰ)求首项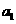 和公比
和公比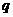 的值;
的值;
(Ⅱ)若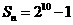 ,求
,求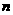 的值.
的值.
14.下面有五个命题:
①函数y=sin4x−−cos4x的最小正周期是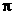 .
②终边在y轴上的角的集合是{a|a=
.
②终边在y轴上的角的集合是{a|a=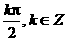 |.
|.
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
④把函数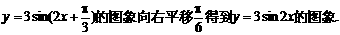
⑤函数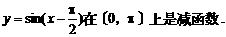 其中真命题的序号 (写出所有真命题的编号)。
其中真命题的序号 (写出所有真命题的编号)。
13.平面内满足不等式组1≤x+y≤3,-1≤x-y≤1,x≥0,y≥0的所有点中,使目标函数z=5x+4y取得最大值的点的坐标是 _____ .
12.已知向量a、b满足:|a|=3,|b|=4,a、b的夹角是120°,则|a+2b|=___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com