
题目列表(包括答案和解析)
3、命题“对任意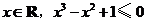 ”的否定是( )
”的否定是( )
A、不存在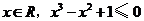 B、存在
B、存在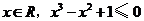
C、存在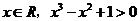 D、对任意的
D、对任意的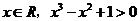
2、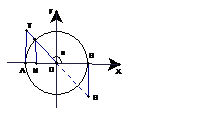 如图所示,角
如图所示,角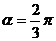 的正切线为有向线段( )
的正切线为有向线段( )
A、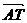 B、
B、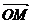 C、
C、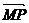 D、
D、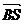
1、设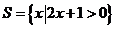 ,
,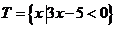 ,则
,则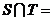 ( )
( )
A、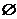 B、
B、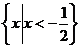 C、
C、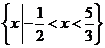 D、
D、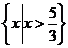
21、(本题满分14分)已知函数
(1)求证: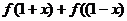 为定值
为定值
(2)求: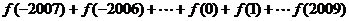 的值;
的值;
(3)设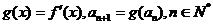 ,且1<a1<2,
,且1<a1<2,
求证: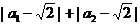 +…+
+…+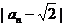 <2.
<2.
20. (本题满分13分)如图,已知双曲线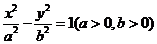 ,其右准线交x轴于点A, 双曲线虚轴的下端点为B,过双曲线的右焦点F
,其右准线交x轴于点A, 双曲线虚轴的下端点为B,过双曲线的右焦点F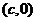 作垂直于x轴的直线交双曲线于点P,若点D满足
作垂直于x轴的直线交双曲线于点P,若点D满足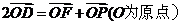
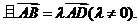
 (1)求双曲线的离心率;
(1)求双曲线的离心率;
(2) 若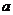 =2,过点B的直线
=2,过点B的直线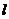 交双曲线于M、N两点,问是否存在
交双曲线于M、N两点,问是否存在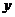 轴上的定点C使
轴上的定点C使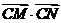 为常数,若存在求出C点的坐标,若不存在,请说明理由.
为常数,若存在求出C点的坐标,若不存在,请说明理由.
19、(本题满分12分)
设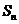 是数列
是数列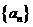 的前n项和,满足
的前n项和,满足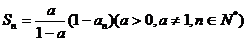 ,数列
,数列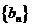 满足
满足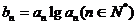 。
。
(1)求数列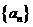 的通项公式;
的通项公式;
(2)若数列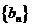 的每一项总小于它后面的项,求a的取值范围。
的每一项总小于它后面的项,求a的取值范围。
18、(本题满分12分)如图,四棱锥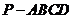 的底面为菱形且∠ABC=120°,PA⊥底面ABCD,AB=1,PA=
的底面为菱形且∠ABC=120°,PA⊥底面ABCD,AB=1,PA=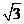 ,E为PC的中点.
,E为PC的中点.
(1)求直线DE与平面PAC所成角的大小;
(2)在线段PC上是否存在一点M,使PC⊥平面MBD成立.并说明理由。
17、(本题满分12分)一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:
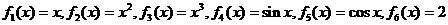
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数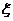 的分布列和数学期望.
的分布列和数学期望.

16、(本题满分12分)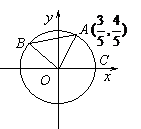 如图
如图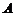 、
、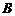 是单位圆
是单位圆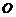 上的点,
上的点,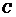 是圆与
是圆与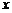 轴正半轴的交点,
轴正半轴的交点, 点的坐标为
点的坐标为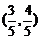 ,三角形
,三角形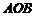 为正三角形.
为正三角形.
(1)求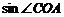 ;
;
(2)求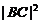 的值.
的值.
15、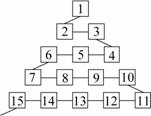 如图是从事网络工作者经常用来解释网络运作的蛇形模型:
如图是从事网络工作者经常用来解释网络运作的蛇形模型:
数字1出现在第1行;数字2,3出现在第2行;数字6,5,4
(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依
此类推.则第99行从左至右算第67个数字为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com