
题目列表(包括答案和解析)
3、函数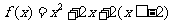 的反函数是 ( B )
的反函数是 ( B )
A. B.
B.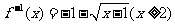
C.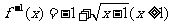 D.
D.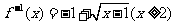
2、在等差数列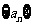 中,
中,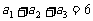 ,
,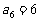 ,则该数列的前7项的和是( C )
,则该数列的前7项的和是( C )
A.14 B.20 C.28 D.56
1、 等于h
( A
)
等于h
( A
)
A.2 B.1 C.-1 D.-2
20.(本题满分16分)
已知二次函数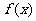 的二次项系数为
的二次项系数为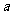 ,且不等式
,且不等式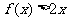 的解集为
的解集为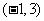 .
.
(1)若方程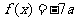 有两个相等的实数根,求
有两个相等的实数根,求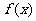 的解析式;
的解析式;
(2)若函数
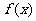 在区间
在区间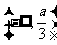 内单调递减,求
内单调递减,求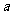 的取值范围;
的取值范围;
(3)当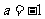 时,证明方程
时,证明方程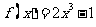 仅有一个实数根.
仅有一个实数根.
19.(本题共16分)
已知AB是椭圆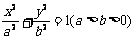 的一条弦,向量
的一条弦,向量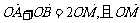 =(2,1)以M为左焦点,以椭圆的右准线为相应准线的双曲线左支与直线AB交于点N(4,-1)
=(2,1)以M为左焦点,以椭圆的右准线为相应准线的双曲线左支与直线AB交于点N(4,-1)
①求椭圆的离心率e1;
②设双曲线的离心率为e2,e1+
e2=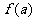 ,求
,求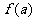 的解析式,并求它的定义域和值域。
的解析式,并求它的定义域和值域。
18.(本题满分15分)
某单位决定投资3200元建一长方体状仓库,高度恒定,它的后墙利用旧墙不花钱,正面用铁珊,每米造价40元,两侧墙砌砖,每米造价45元,顶部每平方米造价20元,计算:
(1)仓库面积S的最大允许值是多少?
(2)为了使仓库面积S达到最大,而实际投资又不超过预算,那么正面用铁珊应设计为多长?
17.(本题满分15分)
如图: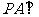 平面
平面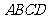 ,四边形
,四边形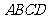 是矩形,
是矩形, ,
,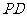 与平面
与平面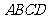 所成的角是
所成的角是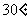 ,点
,点 是
是 的中点,点
的中点,点 在边
在边 上移动.
上移动.
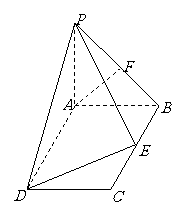 (1)当点
(1)当点 为
为 的中点时,试判断
的中点时,试判断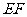 与平面
与平面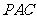 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)证明:不论点 在边
在边 上何处,都有
上何处,都有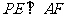 ;
;
16.(本题满分14分)
经统计,某大型商场一个结算窗口每天排队结算的人数及相应的概率如下:
|
排队人数 |
0-5 |
6-10 |
11-15 |
16-20 |
21-25 |
25人以上 |
|
概 率 |
0.1 |
0.15 |
0.25 |
0.25 |
0.2 |
0.05 |
(I)每天不超过20人排队结算的概率是多少?
(Ⅱ)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,商场就需要增加结算窗口,请问该商场是否需要增加结算窗口?
15.(本题满分14分)
在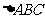 中,
中,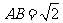 ,
,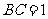 ,
, .
.
(1)求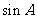 的值;(2)求
的值;(2)求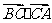 的值.
的值.
14.对正整数n,设抛物线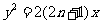 ,过点P(2n,0)任作直线
,过点P(2n,0)任作直线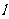 交抛物线于
交抛物线于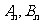 两点,则数列
两点,则数列 的前n 项和为_ _
的前n 项和为_ _
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com