
题目列表(包括答案和解析)
7. 为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文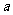 ,
,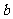 ,
,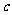 对应密文
对应密文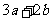 ,
, ,
,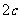 .例如,明文1,2,3对应密文7,14,6. 当
接收方收到密文16,30,14时,则解密得到的明文为
.例如,明文1,2,3对应密文7,14,6. 当
接收方收到密文16,30,14时,则解密得到的明文为
A.2,4,7 B.2,7,4 C.4,2,7 D.7,4,2
6. 函数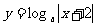 在(-2,0)上是单调递增的,则此函数在
在(-2,0)上是单调递增的,则此函数在 上是
上是
A.单调递增 B.单调递减 C.先增后减 D.先减后增
5. 在△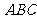 中,若
中,若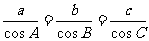 ,则
,则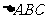 是
是
A.直角三角形 B. 等腰直角三角形
C.钝角三角形 D. 等边三角形
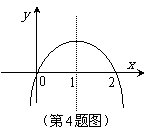
4. 已知函数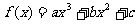 ,其导数
,其导数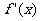 的图象如右图,
的图象如右图,
则函数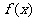 的极小值是
的极小值是
A.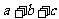 B.
B.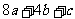 C.
C.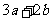 D.
D.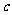
3. 设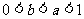 ,则下列不等式成立的是
,则下列不等式成立的是
 A.
A. 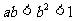 B.
B. 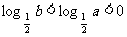
C. 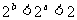 D.
D. 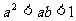
2. 已知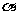 为第二象限的角,且
为第二象限的角,且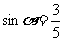 ,则
,则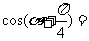
A.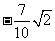 B.
B.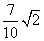 C.
C.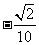 D.
D.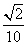
1. 已知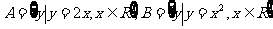 ,则
,则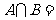
A.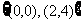 B.
B.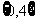 C.
C.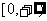 D.
D. 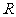
20. (本题满分14分)
已知二次函数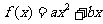 满足条件:
满足条件:
① 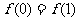 ; ②
; ②
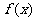 的最小值为
的最小值为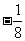 .
.
(1) 求函数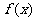 的解析式;
的解析式;
(2) 设数列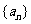 的前
的前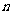 项积为
项积为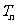 , 且
, 且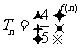 , 求数列
, 求数列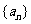 的通项公式;
的通项公式;
(3) 在(2)的条件下, 若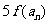 是
是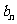 与
与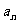 的等差中项, 试问数列
的等差中项, 试问数列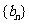 中第几项的值最小? 求出这个最小值.
中第几项的值最小? 求出这个最小值.
19. (本题满分14分)
已知集合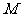 是满足下列性质的函数
是满足下列性质的函数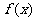 的全体, 存在非零常数
的全体, 存在非零常数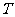 , 对任意
, 对任意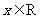 , 有
, 有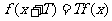 成立.
成立.
(1) 函数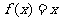 是否属于集合
是否属于集合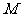 ? 说明理由;
? 说明理由;
(2) 设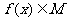 , 且
, 且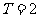 , 已知当
, 已知当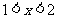 时,
时, 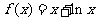 , 求当
, 求当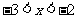 时,
时, 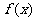 的解析式.
的解析式.
18.(本题满分14分)
设某物体一天中的温度T是时间t的函数,已知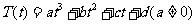 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度T关于时间t的函数关系式;
(2)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com