
题目列表(包括答案和解析)
3.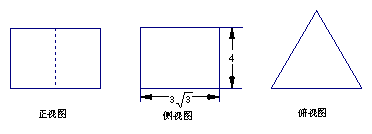 若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为 .
若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为 .
2.设直线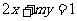 的倾斜角为
的倾斜角为 ,若
,若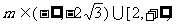 ,则角
,则角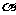 的取值范围是___
的取值范围是___
1.p:“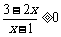 ”和q:“
”和q:“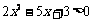 ”,则
”,则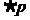 是q的 条件.
是q的 条件.
20.(本题16分)在xOy平面上有一点列P1(a1,b1),P2(a2,b2),…,Pn(an,bn),…,对每个正整数n点Pn位于函数y=2000(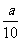 )x(0<a<10)的图象上,且点Pn,点(n,0)与点(n+1,0)构成一个以
)x(0<a<10)的图象上,且点Pn,点(n,0)与点(n+1,0)构成一个以
Pn为顶点的等腰三角形.
(1)求点Pn的纵坐标bn的表达式;
(2)若对于每个正整数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a的取值范围;
(3)设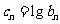 (n∈N*),若a取(2)中确定的范围内的最小整数,问数列{cn}前多少项的和最大?试说明理由.
(n∈N*),若a取(2)中确定的范围内的最小整数,问数列{cn}前多少项的和最大?试说明理由.
答案:(1)由题意知:an=n+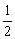 ,∴bn=2000(
,∴bn=2000(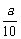 )
)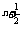 .
.
(2)∵函数y=2000(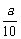 )x(0<a<10)递减,
)x(0<a<10)递减,
∴对每个自然数n,有bn>bn+1>bn+2.则以
bn,bn+1,bn+2为边长能构成一个三角形的充要条件是bn+2+bn+1>bn,
即(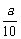 )2+(
)2+(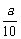 )-1>0,
)-1>0,
解得a<-5(1+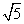 )或a>5(
)或a>5(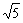 -1).
-1).
∴5(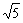 -1)<a<10.
-1)<a<10.
(3)∵5(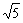 -1)<a<10,∴a=7,∴
-1)<a<10,∴a=7,∴ .
.
∴数列{cn}是一个递减的等差数列,
由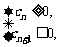 解得
解得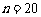 ,故数列{cn}前20项和最大.
,故数列{cn}前20项和最大.
19. (本题16分)已知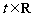 ,函数
,函数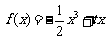
(Ⅰ)当t=1时,求函数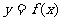 在区间[0,2]的最值;
在区间[0,2]的最值;
(Ⅱ)若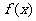 在区间[-2,2]上是单调函数,求t的取值范围;
在区间[-2,2]上是单调函数,求t的取值范围;
(Ⅲ))是否存在常数t,使得任意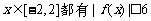 恒成立,若存在,请求出t,若不存在请说明理由.
恒成立,若存在,请求出t,若不存在请说明理由.
答案: (Ⅰ)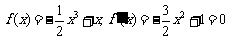 ,
,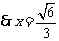 .
.
当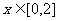 时,
时,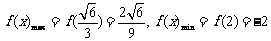 ,
,
(Ⅱ)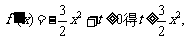
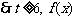 是单调增函数;
是单调增函数;
由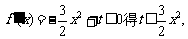
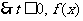 是单调减函数;
是单调减函数;
(Ⅲ)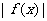 是偶函数,对任意
是偶函数,对任意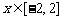 都有
都有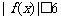 成立,
成立,
故对任意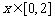 都有
都有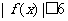 成立
成立
1°由(Ⅱ)知当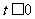 或
或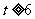 时,
时,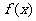 是定义域上的单调函数,
是定义域上的单调函数,
对任意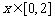 都有
都有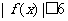 成立
成立
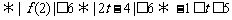
 时,对任意
时,对任意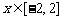 都有
都有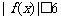 成立.
成立.
2°当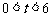 时,
时,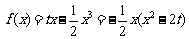 ,由
,由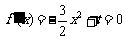 ,
,
得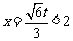 .
.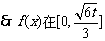 上是单调增函数
上是单调增函数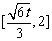 在上是单调减函数,
在上是单调减函数,
∴对任意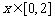 都有
都有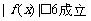
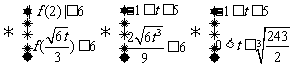 .
.
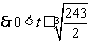 时,对任意
时,对任意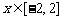 都有
都有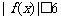 成立.
成立.
综上可知,当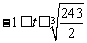 时,对任意
时,对任意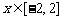 都有
都有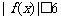 成立.
成立.
18.(本题16分)已知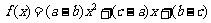 ,且
,且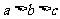 .
.
(1)求证:方程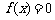 总有两个实根;
总有两个实根;
(2)求不等式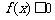 的解集;
的解集;
(3)求使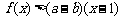 对
对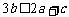 总成立的
总成立的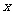 的取值范围.
的取值范围.
[解析]:
(1)解法一: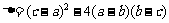
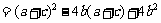
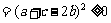 ;又
;又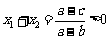 ,
,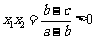
∴方程有两个正根.
解法二: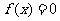

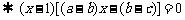 ∴两根为1和
∴两根为1和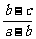 都是正根.
都是正根.
(2)∵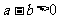 ,∴
,∴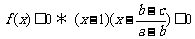 ,
,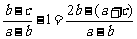
∴若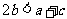 ,则
,则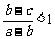 .
.
∴不等式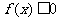 的解集为
的解集为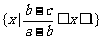 ;
;
若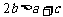 ,解集为
,解集为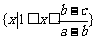 ;
;
若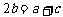 ,解集为
,解集为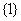 .
.
(3)
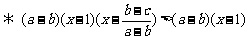
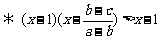
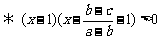
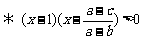 ,∵
,∵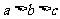 ∴
∴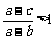
∴不等式的解为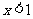 或
或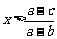
∵当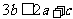 时,
时, 恒成立,
恒成立,
而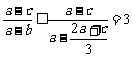
故所求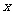 的范围是
的范围是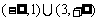 .
.
17. (本题14分)某地区上年度电价为0.8元/kw.h ,年用电量为a kw.h,本年度计划将电价降到0.55元/kw.h至0.75元/.kw.h之间,而用户期望电价是0.4元/kw.h,经测算,下调电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为k),该地区电力的成本是0.3元/kw.h
(1)写出本年度电价下调后,电力部门的收益y与实际电价x的函数关系式;
(2)设k=0.2a,当电价最低定为多少时仍可保证电力部门的收益比上年至少增长20%?
(注:收益=实际用电量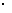 (实际电价 – 成本价))
(实际电价 – 成本价))
答案: (1)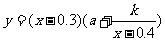
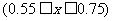
(2)由上年收益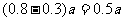
故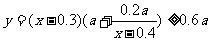
解得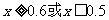
又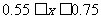
所以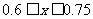
即当电价最低定为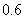 元/kw.h时仍可保证电力部门的收益比
元/kw.h时仍可保证电力部门的收益比
上年至少增长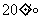 。
。
16.(本题14分)已知定义域为R的函数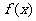 满足
满足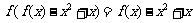 .
.
(1)若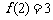 ,求
,求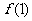 ;又若
;又若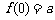 ,求
,求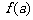 ;
;
(2)设有且仅有一个实数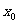 ,使得
,使得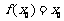 ,求函数
,求函数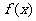 的解析表达式.
的解析表达式.
答案:(1)
∵对任意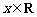 有
有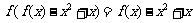 ,
,
∴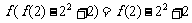 ,又由
,又由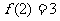 ,∴
,∴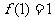 .
.
若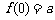 ,∴
,∴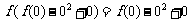 ,即
,即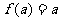 .
.
(2) ∵对任意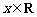 有
有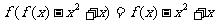 ,
,
又有且仅有一个实数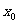 ,使得
,使得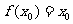 ,
,
∴对任意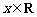 有
有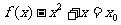 ,
,
在上式中令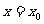 ,有
,有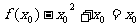 ,
,
又∵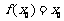 ,∴
,∴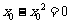 ,
,
即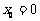 或
或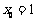 。
。
若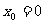 ,则
,则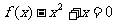 ,即
,即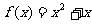 ,
,
但方程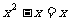 有两个不同的实数根,与题设条件矛盾;
有两个不同的实数根,与题设条件矛盾;
若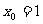 ,则
,则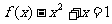 ,即
,即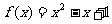 ,满足条件,
,满足条件,
∴满足条件的函数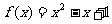 .
.
15.(本题14分)设集合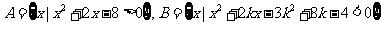 ,若
,若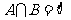 ,求
,求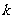 的取值范围.
的取值范围.
答案: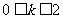
14.若一系列函数的解析式相同,值域相同但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为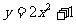 ,值域为
,值域为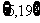 的“孪生函数”共有 ◆ 个。
的“孪生函数”共有 ◆ 个。
答案:9
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com