
题目列表(包括答案和解析)
8、现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为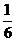 、
、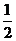 、
、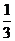 ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是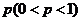 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为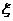 ,对乙项目每投资十万元,
,对乙项目每投资十万元, 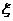 取0、1、2时,
一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量
取0、1、2时,
一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量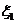 、
、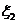 分别表示对甲、乙两项目各投资十万元一年后的利润.
分别表示对甲、乙两项目各投资十万元一年后的利润.
(I) 求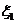 、
、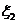 的概率分布和数学期望
的概率分布和数学期望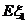 、
、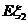 ;
;
(II) 当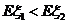 时,求
时,求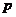 的取值范围.
的取值范围.
7、在医学生物学试验中,经常以果蝇作为试验对象,一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.以ξ表示笼内还剩下的果蝇的只数.
(Ⅰ)写出ξ的分布列(不要求写出计算过程);
(Ⅱ)求数学期望Eξ;
(Ⅲ)求概率P(ξ≥Eξ).
6、已知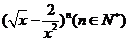 的展开式中第五项的系数与第三项的系数的比是
的展开式中第五项的系数与第三项的系数的比是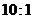 。
。
则展开式中系数最大的项是
三解答题
5、名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号参加团体比赛,则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有_______种.(以数作答)
4、定义:一个没有重复数字的n位正整数(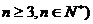 ,各数位上的数字从左到右依次成等差列,称这个数为期望数。则由1,2,3,4,5,6,7,8,9构成四位数中期望的个数为 ( )
,各数位上的数字从左到右依次成等差列,称这个数为期望数。则由1,2,3,4,5,6,7,8,9构成四位数中期望的个数为 ( )
A.9 B.12 C.18 D.20
二填空题
3、已知在1升水中有2只微生物,任取0.1升化验,则取出的0.1升水中含有微生物的概率是( )
A.0.1 B.0.81 C.0.3 D.0.19
2、某种动物由出生算起活到10岁的概率为0.9,活到15岁的概率为0.6.现有一个10岁的这种动物,它能活到15岁的概率是( )
(A)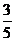 (B)
(B)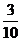 (C)
(C)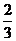 (D)
(D)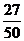
一选择题
1、有6名新生,其中有3名优秀学生,现随机将他们分到三个班级去,每班2人,则每个班都分到优秀学生的概率是( )
A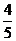 B
B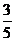 C
C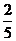 D
D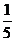
8、已知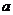 是实数,函数
是实数,函数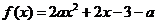 .如果函数
.如果函数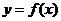 在区间
在区间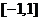 上有
上有
零点,求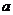 的取值范围.
的取值范围.
7、已知向量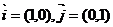 ,规定
,规定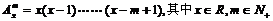 ,且
,且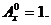 函数
函数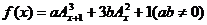 在x=1处取得极值,在x=2处的切线平行于向量
在x=1处取得极值,在x=2处的切线平行于向量 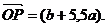
(1)求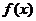 的解析式;
的解析式;
(2)求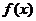 的单调区间;
的单调区间;
(3)是否存在正整数m,使得函数 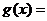
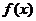
 (
(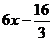 )在区间(m,m+1)内有且只有两个不同零点?若存在,求出m的值;若不存在,说明理由.
)在区间(m,m+1)内有且只有两个不同零点?若存在,求出m的值;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com