
题目列表(包括答案和解析)
1.抛物线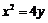 上一点
上一点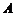 的纵坐标为4,则点
的纵坐标为4,则点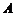 与抛物线焦点的距离为__________
与抛物线焦点的距离为__________
8、解 (1)由题意,2an+1-an=n,又a1=,所以2a2-a1=1,解得a2=,
同理a3=,a4=.
(2)因为2an+1-an=n,
所以bn+1=an+2-an+1-1=-an+1-1=,
bn=an+1-an-1=an+1-(2an+1-n)-1=n-an+1-1=2bn+1,即=
又b1=a2-a1-1=-,所以数列{bn}是以-为首项,为公比的等比数列.
(3)由(2)得,bn=-×()=-3×(),Tn==3×()-.
又an+1=n-1-bn=n-1+3×(),所以an=n-2+3×()n,
所以Sn=-2n+3×=+3-.
由题意,记cn=.要使数列{cn}为等差数列,只要cn+1-cn为常数.
cn===+(3-λ)×,
cn-1=+(3-λ)×,
则cn-cn-1=+(3-λ)×(-).
故当λ=2时,cn-cn-1=为常数,即数列{}为等差数列.
7、Ⅰ)由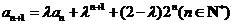 ,
,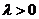 ,
,
可得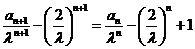 ,
,
所以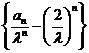 为等差数列,其公差为1,首项为0,故
为等差数列,其公差为1,首项为0,故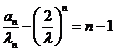 ,所以数列
,所以数列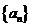 的通项公式为
的通项公式为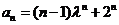 .
.
(Ⅱ)解:设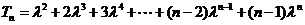 , ①
, ①
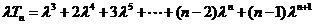 ②
②
当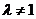 时,①式减去②式,
时,①式减去②式,
得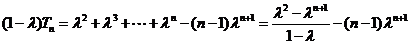 ,
,
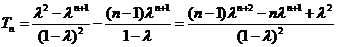 .
.
这时数列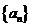 的前
的前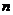 项和
项和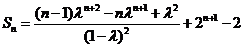 .
.
当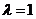 时,
时,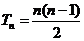 .这时数列
.这时数列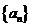 的前
的前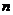 项和
项和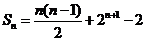 .
.
(Ⅲ)证明:通过分析,推测数列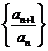 的第一项
的第一项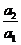 最大,下面证明:
最大,下面证明:
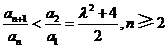 . ③
. ③
由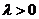 知
知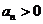 ,要使③式成立,只要
,要使③式成立,只要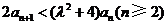 ,
,
因为
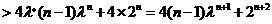
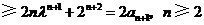 .
.
所以③式成立.
因此,存在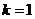 ,使得
,使得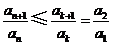 对任意
对任意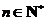 均成立.
均成立.
一选择题BBBC.
二填空题
5、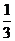 6、(1), (3),
(4)。
6、(1), (3),
(4)。
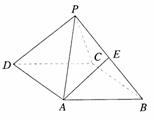
8、如图,在正四棱锥P-ABCD中,E是侧棱PB的中点,侧棱PA与底面ABCD所成角的正切值为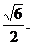
(I)求侧面PAD与底面ABCD所成的二面角的大小;
(II)求异面直线PD与AE所成角的正切值;
(III)在侧面PAD上寻找一点F,使EF⊥侧面PBC,
试确定点F的位置,并证明你找出的点F满足EF⊥侧面PB
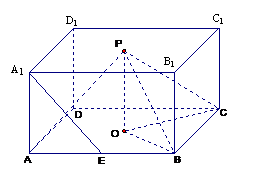
7、如图,O,P分别是正四棱柱ABCD-A1B1C1D1底面中心,E是AB的中点,AB=kAA1,
(Ⅰ)求证:A1E∥平面PBC;
(Ⅱ)当k=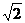 时,求直线PA与平面PBC所成角的大小;
时,求直线PA与平面PBC所成角的大小;
(Ⅲ) 当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?
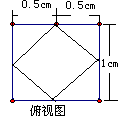
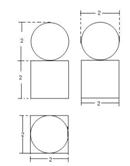
6.根据以下三视图想象物体原形,可得原几何体的体积是 。
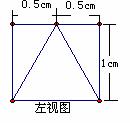
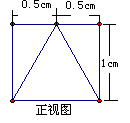 三、解答题
三、解答题
5.已知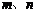 是两条不重合的两条直线,
是两条不重合的两条直线,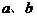 是两个不重合的两个平面,给出以下四个命题:
是两个不重合的两个平面,给出以下四个命题:
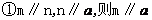 ; ②
; ② 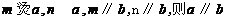 ;
;
③ 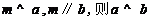 ; ④
; ④ 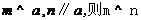 .
.
其中所有正确命题的序号是 .
4.一个几何体的三视图如图所示,则该几何体的体积等于
(A)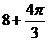 (B)
(B) 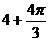
(C) 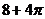 (D)
(D) 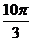
3. 已知:
已知: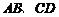 是夹在两平行平面
是夹在两平行平面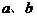 之间的两条线段,
之间的两条线段,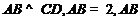 与平面
与平面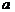 成
成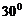 角,则线段
角,则线段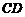 的范围是(
)
的范围是(
)
A 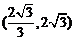 B
B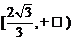 C
C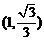 D
D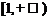
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com