
题目列表(包括答案和解析)
5.
解法一:
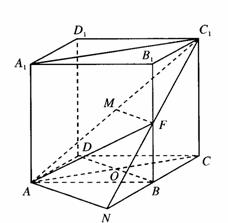
⑴ 延长C1F交CB的延长线于点N,连结AN,因为F是BB1的中点,所以F为C1N的中点,B为CN的中点.
又M是线段AC1的中点,故MF//AN
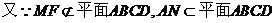
∴ 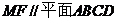
⑵ 证明:连BD,由直四棱柱ABCD-A1B1C1D1可知: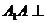 平面ABCD,
平面ABCD,
又∵BD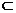 平面ABCD,∴
平面ABCD,∴ 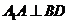
∵ 四边形ABCD为菱形,∴
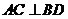
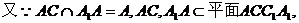
∴ 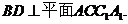
∵ 在四边形DANB中,DA∥BN且DA=BN,
∴ 四边形DANB为平行四边形.
故NA∥BD,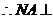 平面ACC1A1.
平面ACC1A1.
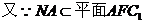 ,
,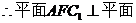 ACC1A1.
ACC1A1.
⑶ 由⑵知BD⊥ACC1A1,又AC1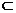 ACC1A1,∴BD⊥AC1,
ACC1A1,∴BD⊥AC1,
∵BD//NA,∴AC1⊥NA.,又由BD⊥AC可知NA⊥AC,
∴∠C1AC就是平面AFC1与平面ABCD所成二面角的平面角或补角
在Rt△C1AC中,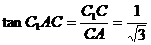 ,故∠C1AC=30°.
,故∠C1AC=30°.
∴平面AFC1与平面ABCD所成二面角的大小为30°或150°.
解法二:
设AC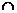 BD=O,因为M、O分别为C1A、CA的中点,所以,MO//C1C,又由直四棱柱知C1C⊥平面ABCD,所以,MO⊥平面ABCD.在棱形ABCD中,BD⊥AC,所以,OB、OC、OM两两垂直.故可以O为原点,OB、OC、OM所在直线分别为
BD=O,因为M、O分别为C1A、CA的中点,所以,MO//C1C,又由直四棱柱知C1C⊥平面ABCD,所以,MO⊥平面ABCD.在棱形ABCD中,BD⊥AC,所以,OB、OC、OM两两垂直.故可以O为原点,OB、OC、OM所在直线分别为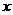 轴、
轴、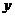 轴、
轴、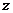 轴如图建立空间直角坐标系,若设|OB|=1,则B(1,0,0),B1(1,0,2),A(0,
轴如图建立空间直角坐标系,若设|OB|=1,则B(1,0,0),B1(1,0,2),A(0,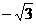 ,0),C(0,
,0),C(0,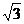 ,0),C1(0,
,0),C1(0,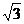 ,2).
,2).


⑴ 由F、M分别为B1B、C1A的中点可知:
F(1,0,1),M(0,0,1),
所以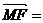 (1,0,0)=
(1,0,0)=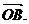
又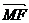 与
与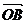 不共线,所以,MF∥OB.
不共线,所以,MF∥OB.
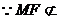 平面ABCD,OB
平面ABCD,OB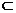 平面ABCD,
平面ABCD,
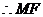 ∥平面ABCD.
∥平面ABCD.
⑵ 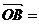 (1,0,0)为平面ACC1A1的法向量.
(1,0,0)为平面ACC1A1的法向量.
设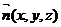 为平面AFC1的一个法向量,则
为平面AFC1的一个法向量,则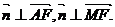
由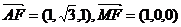 ,
得:
,
得: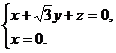
令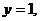 得
得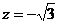 ,此时,
,此时,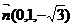 .
.
由于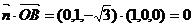 ,所以,平面AFC1⊥平面ACC1A1.
,所以,平面AFC1⊥平面ACC1A1.
⑶ 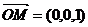 为平面ABCD的法向量,设平面AFC1与平面ABCD所成二面角的大
为平面ABCD的法向量,设平面AFC1与平面ABCD所成二面角的大
小为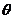 ,则
,则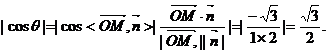
所以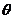 =30°或150°.
=30°或150°.
即平面AFC1与平面ABCD所成二面角的大小为30°或150°.
4.2006年东城区二模文科第17题,理科第16题
解法一:
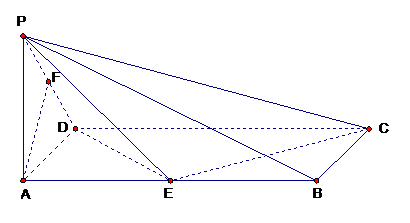
⑴ 取PC的中点O,连结OF、OE.
∴  ,且
,且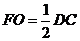 ∴
∴ 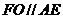
∵ E是AB的中点,且AB=DC, ∴ FO=AE
∴ 四边形AEOF是平行四边形 ∴ AF//OE
又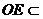 平面PEC,
平面PEC, 平面PEC,
平面PEC,
∴ AF//平面PEC.
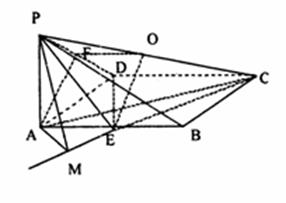
⑵ 连结AC.∵PA⊥平面ABCD,
∴∠PCA是直线PC与平面ABCD所成的角
在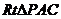 中,
中,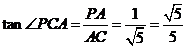
∴ 直线PC与平面ABCD所成角的大小为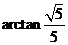 .
.
⑶ 作AM⊥CE,交CE延长线于M,连结PM.
由三垂线定理,得PM⊥CE
∴∠PMA是二面角P-EC-D的平面角.
由△AME-△CBE,可得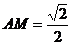
∴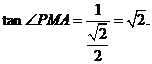
∴ 二面角P-EC-D的大小为 .
.
解法二:
解法二:以A为原点,如图建立直角坐标系.
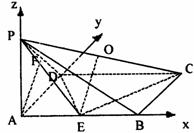

则A(0,0,0),B(2,0,0),C(2,1,0),
D(0,1,0),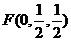 ,E(1,0,0),P(0,0,1).
,E(1,0,0),P(0,0,1).
⑴ 取PC的中点O,连结OE. 则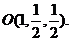
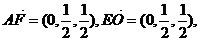
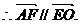
又OE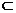 平面PEC,AF
平面PEC,AF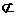 平面PEC,∴AF//平面PEC.
平面PEC,∴AF//平面PEC.
⑵ 由题意可得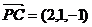 ,
,
设平面ABCD的法向量是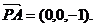
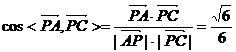
即直线PC与平面ABCD所成角的大小为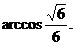
⑶ 设平面PEC的法向量为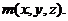
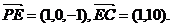
则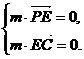 可得
可得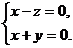
令z= -1,则m=(-1,1,-1).
由(2)可得平面ABCD的法向量是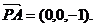
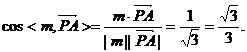
∴二面角P-EC-D的大小为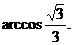
3.
解法一:
⑴ 在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,所以CC1⊥AC.
因为BC=CC1,所以BCC1B1为正方形.
又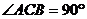 ,所以AC⊥BC,
,所以AC⊥BC,
所以AC⊥平面BCC1B1,
连结B1C,则B1C为AB1在平面BCC1B1上的射影,
 因为B1C⊥BC1,所以AB1⊥BC1.
因为B1C⊥BC1,所以AB1⊥BC1.
⑵ 因为BC//B1C1,BC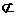 面AB1C1,所以BC//面AB1C1,所以点B到平面AB1C1的距离等于点C到平面AB1C1的距离.
面AB1C1,所以BC//面AB1C1,所以点B到平面AB1C1的距离等于点C到平面AB1C1的距离.
连结A1C交AC1于H,则CH⊥AC1,由于B1C1⊥A1C1,B1C1⊥CC1,所以B1C1⊥平面ACC1A1,B1C1⊥CH,所以CH⊥平面AB1C1,所以CH的长度为点B到平面AB1C1的距离.
因为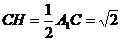 ,所以点B到平面AB1C1的距离为
,所以点B到平面AB1C1的距离为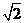 .
.
⑶ 取A1B1中点D,连结C1D.因为△A1B1C1是等腰三角形,所以C1D⊥A1B1,又BB1⊥平面A1B1C1,所以BB1⊥C1D,所以C1D⊥平面ABB1A1.
作DE⊥AB1于E,连C1E,则DE为C1E在平面ABB1A1上的射影,所以C1E⊥AB1,∠C1ED为二面角C1-AB1-A1的平面角.
由已知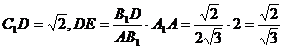 ,
,
∴ 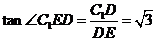 ,
,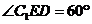
即二面角C1-AB1-A1的大小为60°.
解法二:
⑴ 如图建立直角坐标系,其中C为坐标原点.
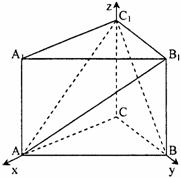

依题意A(2,0,0),B(0,2,0),B1(0,2,2),C1(0,0,2),
因为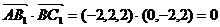 ,所以AB1⊥BC1.
,所以AB1⊥BC1.
⑵ 设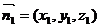 是平面AB1C1的法向量,
是平面AB1C1的法向量,
由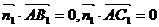 得
得
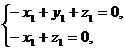 所以
所以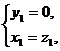
令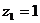 ,则
,则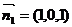 ,
,
因为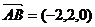 ,所以,B到平面AB1C1的距离为
,所以,B到平面AB1C1的距离为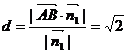 .
.
⑶
设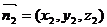 是平面A1AB1的法向量.
是平面A1AB1的法向量.
由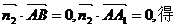
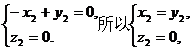 令
令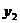 =1,则
=1,则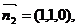
因为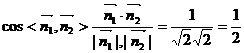 ,
,
所以,二面角C1-AB1-A1的大小为60°.
2.
解法一:
⑴ 取B1C1中点D,连结ND,A1D,所以DN//BB1///AA1又,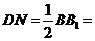
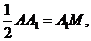 所以四边形A1MND为平行四边形,所以MN//A1D;
所以四边形A1MND为平行四边形,所以MN//A1D;
又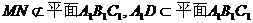 ,所以MN//平面A1B1C1;
,所以MN//平面A1B1C1;
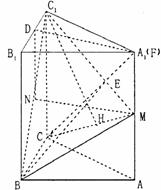
⑵ 三棱柱ABC-A1B1C1为直三棱柱,所以CC1⊥BC,
又∠ACB=90°,所以BC⊥平面A1MC1,
在平面ACC1A中过C1做C1H⊥CM,又BC⊥C1H,所以C1H为C1到平面BMC的距离.
在等三角形CMC1中,CC1=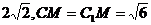 ,
,
所以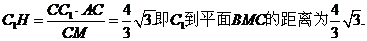
⑶ 在平面ACC1A1上作CF⊥C1M,交C1M于点E,A1C1于点F.则CE为BE在平面ACC1A1上的射影,所以BE⊥CM1,所以∠BEF为二面角B-C1M-A1的平面角.
在等腰三角形CMC1中,CE=C1H=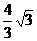 ,
,
所以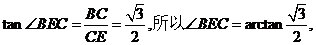
所以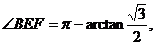
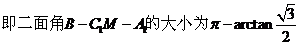 …14分
…14分
解法二:
⑴ 如图,以点C为坐标原点,以CB所在
直线为Ox轴,CA所在直线为Oy轴,CC1所在直线
为Oz轴,建立空间直角坐标系.
由已知得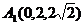 、
、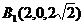 、
、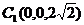 .
.
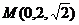 ,
,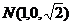 ,
,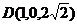
所以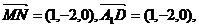
所以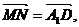 所以MN//A1D;
所以MN//A1D;
又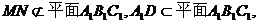 所以MN//平面A1B1C1;
所以MN//平面A1B1C1;
⑵ B(2,0,0)、C(0,0,0),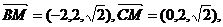
设垂直于平面BCM的向量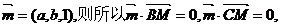
所以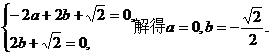 所以
所以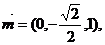
所以C1到平面BMC的距离为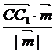
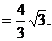
⑶ 三棱柱ABC-A1B1C1为直三棱柱,所以CC1⊥BC,
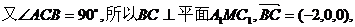
设垂直于平面BMC1的向量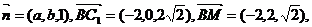
所以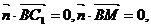 即
即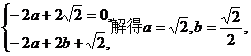
所以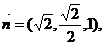
所求二面角的大小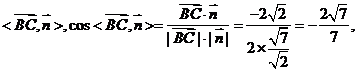
1.
解法一:
⑴ ∵PA⊥底面ABCD,MN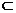 底面ABCD,∴MN⊥PA.
底面ABCD,∴MN⊥PA.
又MN⊥AD,PA∩AD=A, ∴MN⊥平面PAD.
∵MN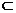 平面PMN,∴平面PMN⊥平面PAD.
平面PMN,∴平面PMN⊥平面PAD.
⑵ ∵BC⊥BA,BC⊥PA,PA∩BA=A,∴BC⊥平面PBA.
∴∠BPC为直线PC与平面PBA所成的角,即sin∠BPC=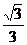 .
.
在Rt△PBC中,PC=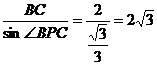 ,
,
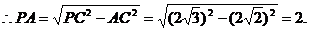
(III)由(I),MN⊥平面PAD,知PM⊥MN,MQ⊥MN,
∴∠PMQ即为二面角P-MN-Q的平面角.
而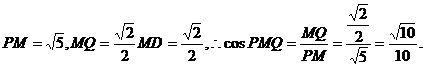
解法二:
⑴ 以A为坐标原点,分别以AB,AD,AP所在的直线为x轴,y轴和z轴,建立空间直角坐标系(图略).
设PA=a,则A(0,0,0),B(2,0,0)C(2,2,0),D(0,2,0)P(0,0,a),
M(0,1,0),N(2,1,0).
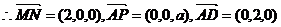
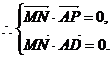 ∴MN⊥平面PAD.
∴MN⊥平面PAD.
∵MN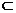 平面PMN,∴平面PMN⊥平面PAD.
平面PMN,∴平面PMN⊥平面PAD.
⑵ 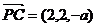 平面PBA的一个法向量为
平面PBA的一个法向量为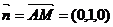 .
.
∵直线PC与平面PBA成角的正弦值为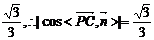
即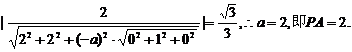
⑶ 同解法一的⑶
6.
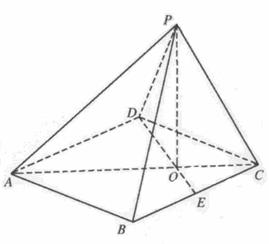
已知四棱锥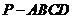 的底面是菱形,
的底面是菱形,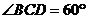 ,
,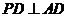 ,点
,点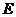 是
是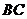 边的中点.
边的中点.
⑴ 求证: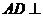 平面
平面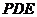 ;
;
⑵ 若二面角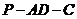 的大小等于
的大小等于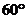 ,且
,且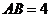 ,
,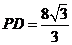 .
.
① 求点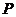 到平面
到平面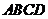 的距离;
的距离;
② 求二面角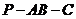 的大小.
的大小.
5.
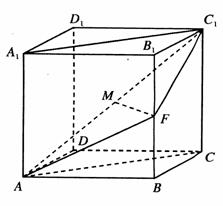
直四棱柱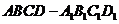 的底面是菱形,且
的底面是菱形,且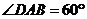 ,
,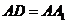 ,
,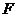 为棱
为棱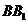 的中点,
的中点,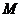 为线段
为线段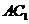 的中点.
的中点.
⑴ 求证:直线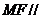 平面
平面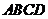 ;
;
⑵ 求证:直线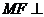 平面
平面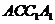 ;
;
⑶求平面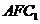 与平面
与平面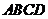 所成二面角的大小.
所成二面角的大小.
4.
已知四棱锥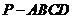 中,底面
中,底面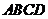 是矩形,
是矩形,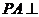 平面
平面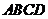 ,
,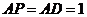 ,
,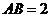 ,
,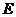 、
、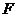 分别是
分别是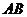 、
、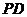 的中点.
的中点.
⑴ 求证: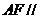 平面
平面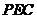 ;
;
⑵ 求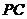 与平面
与平面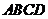 所成角的大小;
所成角的大小;
⑶ 求二面角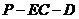 的大小.
的大小.
3.
如图,在直三棱柱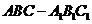 中,
中,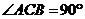 ,
,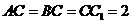
⑴ 证明: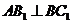 ;
;
⑵ 求点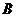 到平面
到平面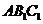 的距离
的距离
⑶ 求二面角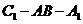 的大小
的大小
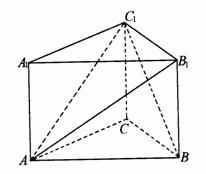
2.
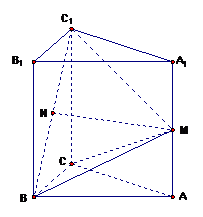
如图,在直三棱柱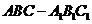 中,
中,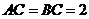 ,
,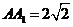 ,
,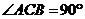 ,
,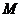 是
是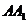 的中点,
的中点,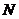 是
是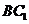 的中点.
的中点.
⑴ 求证: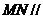 平面
平面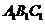 ;
;
⑵ 求点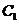 到平面
到平面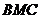 的距离;
的距离;
⑶ 求二面角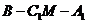 的大小.
的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com