
题目列表(包括答案和解析)
20.某人2000年元月存款t元,按年利息为p的复利计息.计划从2001年开始,每年元月1号到银行提取确定的金额供子女上学使用,恰好在n年后取完.求该人每年提取的金额.
19.数列{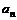 }满足
}满足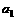 =1,当n∈N*,且n≥2时,
=1,当n∈N*,且n≥2时,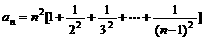 .
.
(1)当n≥2时,求证: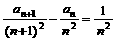 ;
;
(2)比较(1+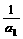 )(1+
)(1+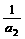 )(1+
)(1+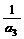 )…(1+
)…(1+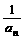 )与4的大小关系.
)与4的大小关系.
18.数列{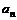 }中,
}中,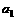 =8,
=8,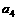 =2,且满足
=2,且满足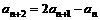 (n∈N*).
(n∈N*).
(1)求数列{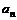 }的通项公式;
}的通项公式;
(2)设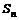 =|
=|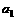 |+|
|+|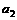 |+…+|
|+…+|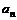 |,求
|,求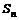 ;
;
(3)设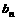 =
=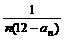 (n∈N*),
(n∈N*),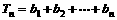 (n∈N*),是否存在最大的整数m,使得对任意n∈N*,均有
(n∈N*),是否存在最大的整数m,使得对任意n∈N*,均有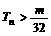 成立?若存在,求出m的值;若不存在,请说明理由.
成立?若存在,求出m的值;若不存在,请说明理由.
17.已知f (x)是定义域在自然数集上的函数,当x为奇数时,有f (x+1)-f (x)=1,当x为偶数时,有f (x+1)-f (x)=3,且f (1)+f (2)=5.
(1)求证:f (1),f (3),…,f (2n-1)(n∈N*)成等差数列;
(2)求f (n)的解析式.
16.一个等比数列{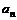 },
},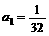 ,前11项的几何平均数是32,若从前11项抽出一项后的几何平均数是16,则抽出的是第
项.
,前11项的几何平均数是32,若从前11项抽出一项后的几何平均数是16,则抽出的是第
项.
15.在公差为d的等差数列{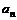 }中有“
}中有“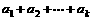 ,
,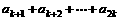 ,…,
,…,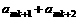 +…+
+…+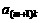 ,…(m、k∈N*)构成公差为
,…(m、k∈N*)构成公差为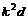 的等差数列”,像这样在公比为q的等比数列{
的等差数列”,像这样在公比为q的等比数列{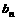 }中有
.
}中有
.
14.三角形的三边长构成等比数列,那么公比q的取值范围是 .
13.无穷数列{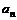 }同时满足条件:
}同时满足条件:
①对任意自然数n∈N*,都有-2<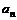 <4;
<4;
②当n为正偶数时,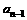 <
<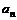 ,且
,且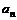 >
>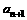 ;
;
③当n>3时,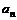 >0.
>0.
请写出一个满足条件的{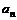 }的通项公式
.
}的通项公式
.
12.数列{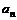 }中任何相邻两项x、y满足
}中任何相邻两项x、y满足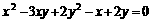 (x,y≠0),那么此数列是 ( )
(x,y≠0),那么此数列是 ( )
A.等差数列 B.等差或等比数列 C.等比数列 D.以上答案都不对
第Ⅱ卷 (非选择题 共90分)
11.等差数列{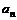 }的首项
}的首项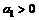 ,前n项的和为
,前n项的和为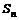 ,若
,若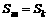 (m、k∈N*且m≠k),则
(m、k∈N*且m≠k),则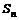 取最大值是 ( )
取最大值是 ( )
A.
n=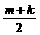
B.n=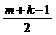
C.当m+k为偶数时,n=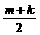 ;当m+k为奇数时,n=
;当m+k为奇数时,n=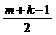
D.当m+k为偶数时,n=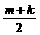 ;当m+k为奇数时,n=
;当m+k为奇数时,n=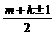
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com