
题目列表(包括答案和解析)
17.(本小题满分13分)
15.(本小题满分13分)
在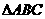 中,角
中,角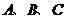 所对的边分别为a,b,c已知向量
所对的边分别为a,b,c已知向量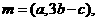
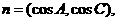 满足
满足
(I)求 的大小;
的大小;
(Ⅱ)求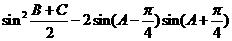 的值
的值
14.对于集合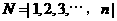 的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减,加后继的数,例如集合|1,2,4,6,9|的交替和是9-6+4-2+1=6,集合
的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减,加后继的数,例如集合|1,2,4,6,9|的交替和是9-6+4-2+1=6,集合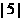 的交替和为5,当集合
的交替和为5,当集合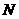 中的
中的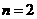 时,集合
时,集合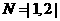 的所有非空子集为|1|,|2|,|1,2|,则它的“交替和”的总和
的所有非空子集为|1|,|2|,|1,2|,则它的“交替和”的总和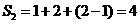 请你尝试对
请你尝试对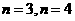 的情况,计算它的“交替和”的总和
的情况,计算它的“交替和”的总和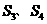 ,并根据其结果猜测集合
,并根据其结果猜测集合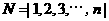 的每一个非空子集的“交替和”的总和
的每一个非空子集的“交替和”的总和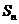 =________________。
=________________。
13.已知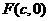 是椭圆
是椭圆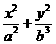 =1(
=1(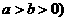 的右焦点,以坐标原点
的右焦点,以坐标原点 为圆心,
为圆心,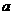 为半径作圆
为半径作圆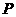 ,过
,过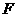 垂直于
垂直于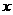 轴的直线与圆
轴的直线与圆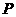 交于
交于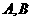 两点,过点
两点,过点 作圆
作圆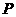 的切线交
的切线交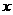 轴于点
轴于点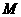 若直线
若直线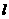 过点
过点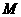 且垂直于
且垂直于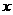 轴,则直线
轴,则直线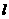 的方程为_______________________;若
的方程为_______________________;若 =
=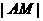 ,则椭圆的离心率等于______________。
,则椭圆的离心率等于______________。
12.设集合 ,定义在
,定义在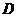 上的映射
上的映射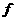 ,满足对任意
,满足对任意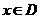 ,均有
,均有
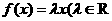 且
且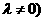 ,若
,若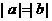
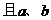 不共线,则
不共线,则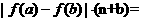 ______;
______;
若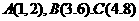 ,且
,且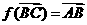 ,则
,则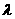 =____________________________。
=____________________________。
11.如图,等腰梯形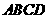 中,
中,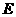 ,
,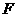 分别是
分别是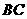 上三等分点,
上三等分点,
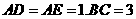 ,若把三角形
,若把三角形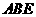 和
和 分别沿
分别沿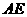
和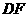 折起,使得
折起,使得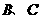 两点重合于一点
两点重合于一点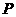 ,则二面角
,则二面角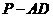
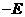 的大小为_________________________
的大小为_________________________
10. 极限
极限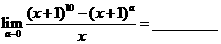
9.已知 是复数,i是虚数单位,若
是复数,i是虚数单位,若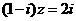 ,则
,则 =__________________________
=__________________________
8.已知函数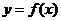 的定义域为
的定义域为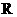 ,当
,当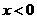 时,
时,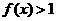 ,且对任意的
,且对任意的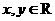 ,等式
,等式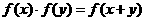 成立,若数列
成立,若数列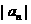 满足
满足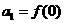 ,且
,且
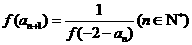 则
则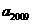 的值为
的值为
A.4016 B.4017 C.4018 D.4019
7.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数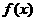 的图象恰好通过
的图象恰好通过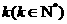 个格点,则称函数
个格点,则称函数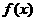 为
为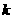 阶格点函数,下列函数:
阶格点函数,下列函数:
①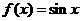 ; ②
; ②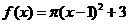 ; ③
; ③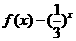 ; ④
; ④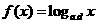
其中是一阶格点函数的有
A.①② B.①④ C.①②④ D.①②③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com