
题目列表(包括答案和解析)
8. (命题人:如东中学洪兵,审题人:如东中学何鹏 ,原创)
已知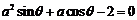 ,
,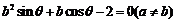 ,对任意
,对任意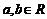 ,经过两点
,经过两点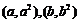 的直线与一定圆相切,则圆方程为 .
的直线与一定圆相切,则圆方程为 .
[解析]经过两点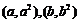 的直线方程为
的直线方程为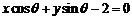 .
.
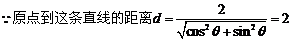 ,
,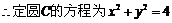 .
.
7. (命题人:如东中学何鹏,审题人:如东中学缪林,原创 )
用单位立方块搭一个几何体,使它的主视图和俯视图如右图所示,
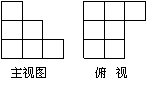 则它的体积的最大值与最小值之差为 .
则它的体积的最大值与最小值之差为 .
[解析]6.体积的最大值为16,体积最小值为10.
6. (命题人:启东中学顾晏辉,审题人:启东中学李俊)
己知:函数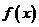 满足
满足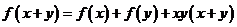 ,又
,又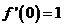 .则函数
.则函数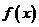 的解析式为
.
的解析式为
.
[解析]由已知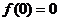 ,当
,当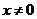 时,原方程化为
时,原方程化为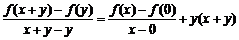 .
.
由等式右边存在极限,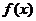 处处可导.
处处可导.
对原方程两边令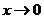 ,得
,得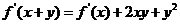 .
.
令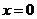 ,
,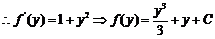 (
(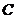 为常数).
为常数).
又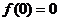 ,得
,得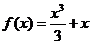 .
.
5. (命题人:启东中学胡勇,审题人:启东中学李俊)
已知命题P:.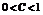 ,
,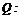 不等式
不等式 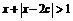 的解集为
的解集为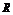 .如果
.如果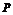 和
和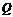 有且仅有一个正确,则
有且仅有一个正确,则 的取值范围是
.
的取值范围是
.
[解析]若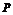 和
和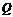 都正确,则由
都正确,则由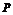 ,有
,有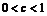 .由
.由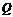 ,有
,有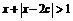 的解集为
的解集为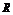 .
.
用函数认识不等式,只需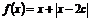 的最小值
的最小值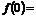 2
2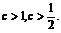 此时
此时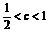 .
.
若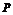 和
和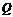 都不正确,则由
都不正确,则由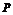 ,有
,有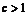 .由
.由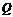 ,有
,有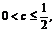 其交集为空集,此时
其交集为空集,此时 不存在.
不存在.
由题设知,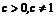 ,用补集思想,所求
,用补集思想,所求 的取值范围为
的取值范围为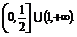 .
.
4. (命题人:启东中学俞向阳,审题人:启东中学李俊)
设函数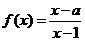 ,集合M=
,集合M=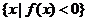 ,P=
,P=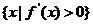 ,若M
,若M P,则实数a的取值范围是
.
P,则实数a的取值范围是
.
[解析]设函数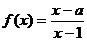 , 集合
, 集合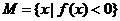 .
.
若a>1时,M={x| 1<x<a};
若a<1时,M={x| a<x<1};
a=1时,M=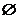 .
.
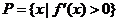 ,∴
,∴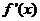 =
=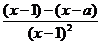 >0.
>0.
∴ a>1时,P=R,a<1时,P=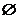 ;已知
;已知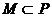 ,所以 (1,+∞).
,所以 (1,+∞).
3. (命题人:启东中学李俊,审题人:启东中学曹瑞彬,原创)
已知单位正方体ABCD-A1B1C1D1对棱BB1,DD1上有两个动点E、F,BE=D1F,设EF与面AB1所成角为α,与面BC1所成角为β,则α+β的最大值为 .
[解析]由对称性可知α=β,又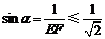 ,所以α≤45°,α+β≤90°.
,所以α≤45°,α+β≤90°.
2. (命题人:启东中学曹瑞彬,审题人:启东中学李俊,原创)
在△ABC中,角A、B、C的对边分别为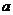 、
、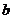 、
、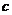 ,且
,且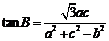 ,则角B的大小是
.
,则角B的大小是
.
[解析]由余弦定理,得 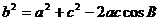 .则
.则
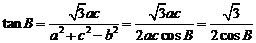 ,即
,即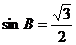 .
.
所以B的大小是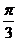 或
或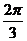 .
.
1. (命题人:启东中学曹瑞彬,审题人:启东中学李俊,原创)
若曲线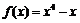 在点P处的切线平行于直线3x-y=0,则点P的坐标为
.
在点P处的切线平行于直线3x-y=0,则点P的坐标为
.
[解析]设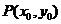 ,由
,由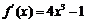 ,得
,得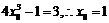 ,从而
,从而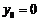 .
.
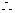 点P的坐标为(1,0).
点P的坐标为(1,0).
21.本题有(1) 、(2) 、(3)三个选考题,每题7分,请考生任选2题作答,满分14分.如果多做,则所做的前两题计分.
(1)(本小题满分7分)选修4-2:矩阵与变换.
求曲线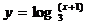 在
在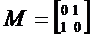 作用下变换的曲线方程
作用下变换的曲线方程
(2)(本小题满分7分)选修4-4:坐标系与参数方程.
过点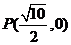 作倾斜角为
作倾斜角为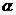 的直线与曲线
的直线与曲线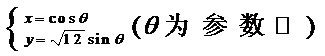 交于点
交于点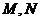 ,
,
求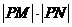 的最小值及相应的
的最小值及相应的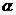 的值.
的值.
(3)(本小题满分7分)选修4-5:不等式选讲.
解不等式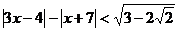
20.(本小题满分14分)
已知函数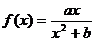 在
在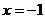 处取得极值-2.
处取得极值-2.
(1)求函数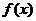 的表达式;
的表达式;
(2)当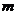 满足什么条件时,函数
满足什么条件时,函数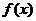 在区间
在区间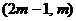 上单调递增?
上单调递增?
(3)若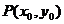 为
为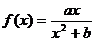 图象上任意一点,直线
图象上任意一点,直线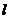 与
与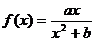 的图象切于点
的图象切于点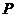 ,设直线
,设直线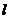 的斜率
的斜率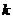 ,求函数
,求函数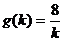 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com