
题目列表(包括答案和解析)
1.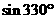
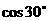 等于( )
等于( )
A.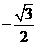 B.
B.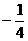 C.
C.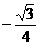 D.
D.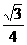
22.(本小题满分14分)
已知椭圆C: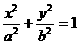 (a>b>0)的离心率为
(a>b>0)的离心率为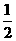 ,直线
,直线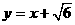 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
(I)求椭圆C的方程;
(II)若直线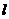 :
: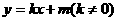 与椭圆C交于不同的两点M,N,且线段MN的垂直平分线过定点G(
与椭圆C交于不同的两点M,N,且线段MN的垂直平分线过定点G(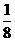 ,0),求实数k的取值范围.
,0),求实数k的取值范围.
21.(本小题满分12分) 已知函数f(x)=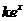 -x.
-x.
(I)当k=1时,试确定函数f(x)单调区间;
(Ⅱ)若对任意x∈R,有,f(x)>0恒成立,求实数k的取值范围.
20.(本小题满分12分)
某班t名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组,第一组[13,14);第二组[14,15)…第五组[17,18],下表是按上述分组方法得到的频率分布表:
|
分组 |
频数 |
频率 |
|
[13,14) |
X |
0.04 |
|
[14,15) |
9 |
y |
|
[15,16) |
z |
0.38 |
|
[16,17) |
16 |
0.32 |
|
[17,18] |
4 |
0.08 |
(I)求t及分布表中x,y,z的值;
(Ⅱ)设m,n是从第一组或第五组中任意抽取的两名学生的百米测试成绩,求事件“|m-n|>1”的概率.
19.(本小题满分12分)
已知四棱柱ABCD-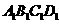 的侧棱A
的侧棱A 。垂直于底面,底面ABCD为直角梯形,AD∥BC,AB
。垂直于底面,底面ABCD为直角梯形,AD∥BC,AB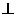 BC,AD=A
BC,AD=A =2,AB=BC=1,E,F分别为
=2,AB=BC=1,E,F分别为 D,CD中点.
D,CD中点.
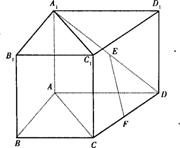 (I)求证:EF∥平面
(I)求证:EF∥平面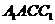 ;
;
(Ⅱ)求证:CD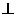 平面
平面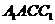 ,并求四棱锥D-
,并求四棱锥D-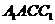 的体积
的体积
18.(本小题满分12分)
数列(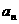 )是首项
)是首项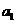 =4的等比数列,
=4的等比数列, 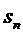 为其前n项和,且
为其前n项和,且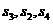 成等差数列.
成等差数列.
(I)求数列{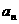 }的通项公式;
}的通项公式;
(II)若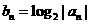 ,设
,设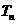 为数列{
为数列{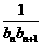 }的前n项和,求证
}的前n项和,求证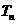 <
<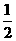
17.(本小题满分12分)
已知函数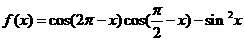
(I)求函数f(x)的最小正周期;(II)当x∈[-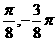 ]时,求函数,f(x)的值域.
]时,求函数,f(x)的值域.
16. 设z=x+y,其中 x,y满足
设z=x+y,其中 x,y满足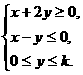 若z的最小值为-3,则z的最大值为
.
若z的最小值为-3,则z的最大值为
.
15.已知x>0,y>0,且-1,x,4,y,6的平均数为2,则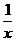 +
+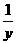 的最小值为
.
的最小值为
.
14.已知函数y=x1nx,则这个函数在点x=1处的切线方程是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com