
题目列表(包括答案和解析)
9.若直三角形的周长为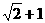 ,则它的最大面积为__________.
,则它的最大面积为__________.
解析:设两条直角边长为a,b,则斜边长为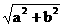 .
.
依题设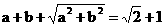 ,
,
因为a+b≥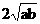 且a2+b2≥2ab,
且a2+b2≥2ab,
所以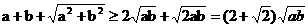 ,
,
即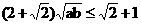 .
.
于是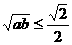 ,即
,即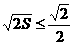 ,所以S≤
,所以S≤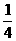 ,
,
当且仅当a=b时,等号成立.
故Smax=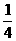 .
.
答案: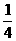
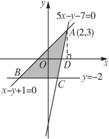
8.当实数x、y满足约束条件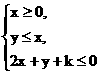 (k为常数)时,z=x+3y有最大值为12,则实数k的值是____________________
(k为常数)时,z=x+3y有最大值为12,则实数k的值是____________________
解析:画出可行域,由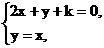 得交点(
得交点(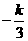 ,
,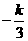 ).
).
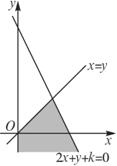
由图观察知在点(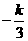 ,
,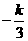 )处,z=x+3y取得最大值12,
)处,z=x+3y取得最大值12,
于是有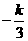 +3×(
+3×(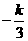 )=12,解得k=-9.
)=12,解得k=-9.
答案:-9
7.若关于x的不等式|x+3|+|x-1|>a恒成立,则a的取值范围是________.
解析:从几何角度看,不等式左侧表示数轴上到点-3和点1的距离之和,最小值为4,故a<4.
答案:a<4
6.设A、B是两个集合,定义A-B={x|x∈A且x B}.
B}.
若A={x||x-1|≤3},B={x|x=3|cosα|,α∈R},则A-B=______________.
解析:由|x-1|≤3得-2≤x≤4,
∴A={x|-2≤x≤4};
由x=3|cosα|∈[0,3]知B={x|0≤x≤3}.
由定义A-B={x|x∈A且x B},得A-B=[-2,0)∪(3,4].
B},得A-B=[-2,0)∪(3,4].
答案:[-2,0)∪(3,4]
5.设O为坐标原点,M(2,1),若点N(x,y)满足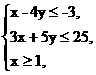 则|
则|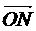 |cos∠MON的最大值为…( )
|cos∠MON的最大值为…( )
A.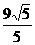 B.
B.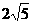 C.
C.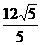 D.
D.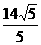
解析:由向量的投影的定义可知|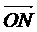 |cos∠MON=
|cos∠MON=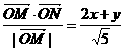 ,令z=2x+y,作出可行域,易得在点(5,2)处目标函数z=2x+y取得最大值12,故|
,令z=2x+y,作出可行域,易得在点(5,2)处目标函数z=2x+y取得最大值12,故|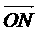 |cos∠MON的最大值为
|cos∠MON的最大值为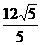 .
.
答案:C
4.若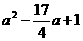 <0,则不等式x2+ax+1>2x+a成立的x的取值范围是( )
<0,则不等式x2+ax+1>2x+a成立的x的取值范围是( )
A.{x|x≥3或x≤1}
B.{x|x<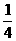 或x>4}
或x>4}
C.{x|1<x<3} D.{x|x≤-3或x>1}
解析:由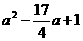 <0,得a∈(
<0,得a∈(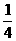 ,4).
,4).
由x2+ax+1>2x+a,得[x-(1-a)]·(x-1)>0.
∴x<1-a或x>1.
∴x≤-3或x>1.
答案:D
3.不等式|2x-log2x|<|2x+log2x|的解集是( )
A.(1,2) B.(0,1) C.(1,+∞) D.(2,+∞)
解析:两边平方,得4x2-4xlog2x+log22x<4x2+4xlog2x+log22x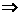 xlog2x>0
xlog2x>0
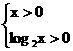
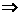 x>1,
x>1,
∴选C.
答案:C
2.不等式|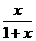 |>
|>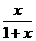 的解集是( )
的解集是( )
A.{x|x≠-1} B.{x|x>-1} C.{x|x<0且x≠-1} D.{x|-1<x<0}
解析:∵|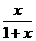 |>
|>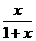 ,∴
,∴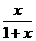 <0,即x(1+x)<0.∴-1<x<0.∴选D.
<0,即x(1+x)<0.∴-1<x<0.∴选D.
答案:D
1.已知0<a<1,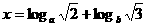 ,y=
,y=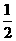 loga5,
loga5,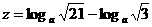 ,则…( )
,则…( )
A.x>y>z B.z>y>x C.y>x>z D.z>x>y
解析:∵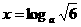 ,
,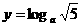 ,
,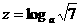 ,由0<a<1知其为减函数,
,由0<a<1知其为减函数,
∴y>x>z.
答案:C
13.预算用2 000元购买单件为50元的桌子和20元的椅子,希望使桌子和椅子的总数尽可能得多,但椅子不少于桌子数,且不多于桌子数的1.5倍,问桌子、椅子各买多少才行?
解:设桌、椅分别买x张、y把,目标函数z=x+y,把所给的条件表示成不等式组,即约束条件为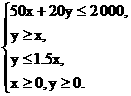 由
由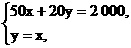
解得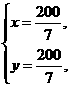 所以A点的坐标为(
所以A点的坐标为(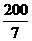 ,
,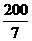 ).
).
由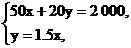 解得
解得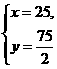
所以B点的坐标为(25,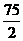 ).
).
所以满足条件的可行域是以A(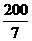 ,
,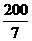 ),B(25,
),B(25,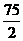 ),O(0,0)为顶点的三角形区域(如下图),由图形可知,目标函数z=x+y在可行域内的最优解为(25,
),O(0,0)为顶点的三角形区域(如下图),由图形可知,目标函数z=x+y在可行域内的最优解为(25,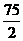 ),但注意到x∈N*,y∈N*,故取
),但注意到x∈N*,y∈N*,故取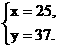
故买桌子25张,椅子37把是最好的选择.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com