
题目列表(包括答案和解析)
6.(2008海南、宁夏高考,理6)已知a1>a2>a3>0,则使得(1-aix)2<1(i=1,2,3)都成立的x的取值范围是( )
A.(0,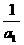 ) B.(0,
) B.(0,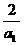 )
C.(0,
)
C.(0,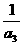 )
D.(0,
)
D.(0,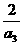 )
)
解析:由(1-aix)2<1(i=1,2,3),得1-2aix+ai2x2<1,即x(ai2x-2ai)<0(i=1,2,3),
解之,得0<x<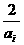 (ai>0),由于a1>a2>a3>0,故0<x<
(ai>0),由于a1>a2>a3>0,故0<x<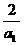 ,选B.
,选B.
答案:B
5.已知集合A={x|3x-2-x2<0},B={x|x-a<0},且B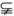 A,则实数a的取值范围是( )
A,则实数a的取值范围是( )
A.a≤1 B.1<a≤2 C.a>2 D.a≤2
解析:不等式3x-2-x2<0化为x2-3x+2>0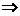 x>2或x<1,由不等式x-a<0,得x<a.要使B
x>2或x<1,由不等式x-a<0,得x<a.要使B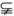 A,则a≤1.
A,则a≤1.
答案:A
4.不等式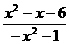 >0的解集是( )
>0的解集是( )
A.{x|-2<x<3} B.{x|x≤-2或x≥3}
C.{x|x<-2} D.{x|x>3}
解析:不等式化为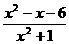 <0,所以x2-x-6<0
<0,所以x2-x-6<0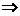 -2<x<3.
-2<x<3.
答案:A
3.(2008四川高考,文5)不等式|x2-x|<2的解集为( )
A.(-1,2) B.(-1,1) C.(-2,1) D.(-2,2)
解析:∵|x2-x|<2,
∴-2<x2-x<2,
即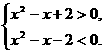
解得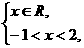
∴x∈(-1,2),故选A.
答案:A
2.设不等式|x-a|<b的解集为{x|-1<x<2},则a与b的值分别为( )
A.1,3
B.-1,3 C.-1,-3 D.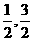
解析:不等式|x-a|<b的解集为{x|a-b<x<a+b},又∵不等式|x-a|<b的解集为{x|-1<x<2},则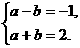
∴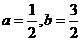
答案:D
1.不等式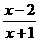 ≤0的解集是( )
≤0的解集是( )
A.(-∞,-1)∪(-1,2] B.[-1,2] C.(-∞,-1)∪[2,+∞) D.(-1,2]
解析:由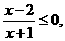 得
得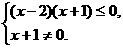
所以不等式的解集为(-1,2].
答案:D
19.已知函数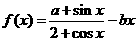
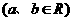 ,
,
(Ⅰ)若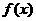 在
在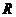 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为 ,试求
,试求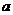 和
和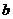 的值。
的值。
(Ⅱ)若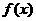 为奇函数,(1)是否存在实数
为奇函数,(1)是否存在实数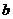 ,使得
,使得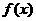 在
在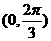 为增函数,
为增函数,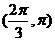 为减函数,若存在,求出
为减函数,若存在,求出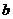 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当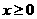 时,都有
时,都有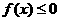 恒成立,试求
恒成立,试求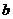 的取值范围。
的取值范围。
18.各项均为正数的数列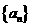 的前
的前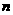 项和为
项和为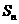 ,
,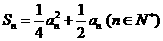 ;
;
(1)求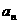 ;(2)令
;(2)令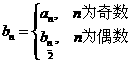 ,
,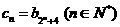 ;求
;求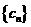 的前
的前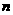 项和
项和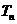 。
。
(3)令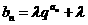 (
(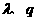 为常数,
为常数,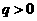 且
且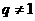 ),
),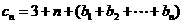 ,
,
是否存在实数对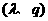 ,使得数列
,使得数列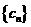 成等比数列?
成等比数列?
若存在,求出实数对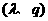 及数列
及数列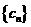 的通项公式,若不存在,请说明理由。
的通项公式,若不存在,请说明理由。
17.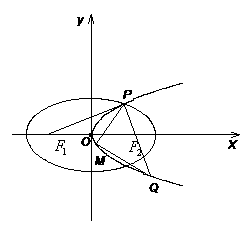 .如图,设抛物线
.如图,设抛物线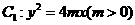 的准线与
的准线与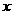 轴交于
轴交于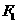 ,焦点为
,焦点为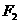 ;以
;以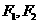 为焦点,离心率
为焦点,离心率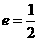 的椭圆
的椭圆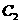 与抛物线
与抛物线 在
在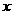 轴上方的交点为
轴上方的交点为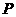 ,延长
,延长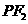 交抛物线于点
交抛物线于点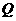 ,
,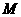 是抛物线
是抛物线 上一动点,且M在
上一动点,且M在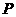 与
与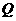 之间运动.
之间运动.
(1)当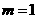 时,求椭圆
时,求椭圆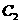 的方程;
的方程;
(2)当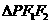 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求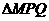 面积的最大值.
面积的最大值.
16.如图,直三棱柱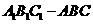 中,
中,
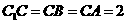 ,
,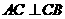 .
. 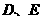 分别为棱
分别为棱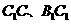 的中点.
的中点.
(1)求点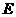 到平面
到平面 的距离;(2)求二面角
的距离;(2)求二面角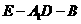 的平面角的余弦值;
的平面角的余弦值;
(3)在线段 上是否存在一点
上是否存在一点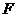 ,使得
,使得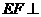 平面
平面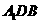 ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com