
题目列表(包括答案和解析)
8.设不等式组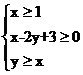 所表示的平面区域是
所表示的平面区域是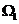 ,平面区域是
,平面区域是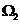 与
与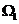 关于直线
关于直线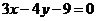 对称,对于
对称,对于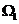 中的任意一点A与
中的任意一点A与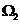 中的任意一点B,
中的任意一点B, 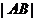 的最小值等于( )
的最小值等于( )
A.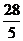 B.4 C.
B.4 C.
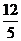 D.2
D.2
[答案]B
[解析]由题意知,所求的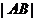 的最小值,即为区域
的最小值,即为区域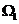 中的点到直线
中的点到直线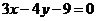 的距离的最小值的两倍,画出已知不等式表示的平面区域,如图所示,
的距离的最小值的两倍,画出已知不等式表示的平面区域,如图所示,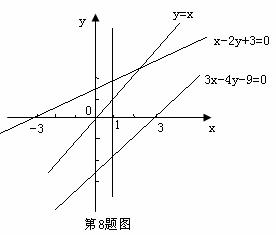
可看出点(1,1)到直线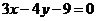 的距离最小,故
的距离最小,故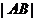 的最小值为
的最小值为
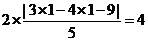 ,所以选B。
,所以选B。
 A. ①④ B.
②③ C.②④ D.③④
A. ①④ B.
②③ C.②④ D.③④
[答案]C
[解析]经分析容易得出②④正确,故选C。
[命题意图]本题属新题型,考查函数的相关知识。
7.若点O和点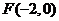 分别是双曲线
分别是双曲线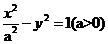 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则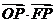 的取值范围为 ( )
的取值范围为 ( )
A.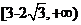 B.
B.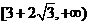 C.
C.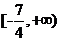 D.
D.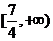
[答案]B
[解析]因为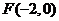 是已知双曲线的左焦点,所以
是已知双曲线的左焦点,所以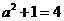 ,即
,即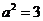 ,所以双曲线方程为
,所以双曲线方程为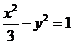 ,设点P
,设点P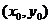 ,则有
,则有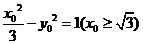 ,解得
,解得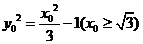 ,因为
,因为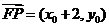 ,
,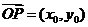 ,所以
,所以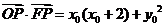 =
=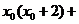
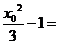
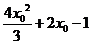 ,此二次函数对应的抛物线的对称轴为
,此二次函数对应的抛物线的对称轴为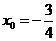 ,因为
,因为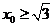 ,所以当
,所以当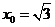 时,
时,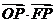 取得最小值
取得最小值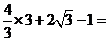
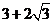 ,故
,故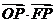 的取值范围是
的取值范围是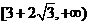 ,选B。
,选B。
[命题意图]本题考查待定系数法求双曲线方程,考查平面向量的数量积的坐标运算、二次函数的单调性与最值等,考查了同学们对基础知识的熟练程序以及知识的综合应用能力、运算能力。
4.函数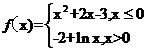 的零点个数为 ( )
的零点个数为 ( )
A.0 B.1 C.2 D.3
[答案]C
[解析]当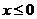 时,令
时,令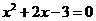 解得
解得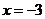 ;
;
当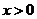 时,令
时,令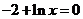 解得
解得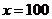 ,所以已知函数有两个零点,选C。
,所以已知函数有两个零点,选C。
[命题意图]本题考查分段函数零点的求法,考查了分类讨论的数学思想。
 所以
所以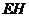 ∥
∥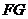 ,故
,故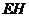 ∥
∥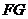 ∥
∥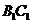 ,所以选项A、C正确;因为
,所以选项A、C正确;因为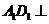 平面
平面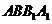 ,
,
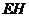 ∥
∥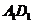 ,所以
,所以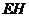
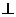 平面
平面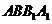 ,又
,又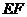
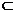 平面
平面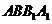 , 故
, 故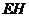
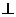
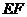 ,所以选项B也正确,故选D。
,所以选项B也正确,故选D。
[命题意图]本题考查空间中直线与平面平行、垂直的判定与性质,考查同学们的空间想象能力和逻辑推理能力。
3.设等差数列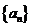 的前n项和为
的前n项和为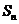 ,若
,若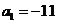 ,
,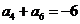 ,则当
,则当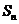 取最小值时,n等于
取最小值时,n等于
A.6 B.7 C.8 D.9
[答案]A
[解析]设该数列的公差为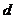 ,则
,则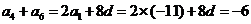 ,解得
,解得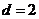 ,
,
所以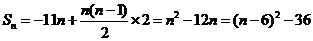 ,所以当
,所以当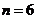 时,
时,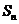 取最小值。
取最小值。
[命题意图]本题考查等差数列的通项公式以及前n项和公式的应用,考查二次函数最值的求法及计算能力。
2.以抛物线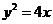 的焦点为圆心,且过坐标原点的圆的方程为(
)
的焦点为圆心,且过坐标原点的圆的方程为(
)
A.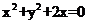 B.
B.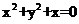 C.
C.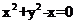 D.
D.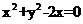
[答案]D
[解析]因为已知抛物线的焦点坐标为(1,0),即所求圆的圆心,又圆过原点,所以圆的半径为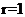 ,故所求圆的方程为
,故所求圆的方程为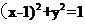 ,即
,即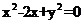 ,选D。
,选D。
[命题意图]本题考查抛物线的几何性质以及圆的方程的求法,属基础题。
1.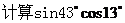
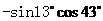 的值等于( )
的值等于( )
A.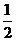 B.
B.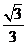 C.
C.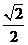 D.
D.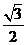
[答案]A
[解析]原式=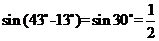 ,故选A。
,故选A。
[命题意图]本题考查三角函数中两角差的正弦公式以及特殊角的三角函数,考查基础知识,属保分题。
(17)(本小题满分12分)
已知函数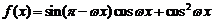 (
(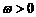 )的最小正周期为
)的最小正周期为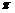 ,
,
(Ⅰ)求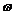 的值;
的值;
(Ⅱ)将函数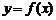 的图像上各点的横坐标缩短到原来的
的图像上各点的横坐标缩短到原来的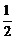 ,纵坐标不变,得到函数
,纵坐标不变,得到函数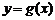 的图像,求函数
的图像,求函数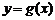 在区间
在区间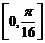 上的最小值.
上的最小值.
(18)(本小题满分12分)
已知等差数列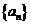 满足:
满足: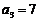 ,
,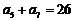 .
.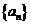 的前n项和为
的前n项和为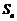 .
.
(Ⅰ)求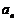 及
及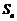 ;
;
(Ⅱ)令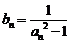 (
(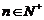 ),求数列
),求数列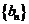 的前n项和
的前n项和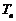 .
.
(19)(本小题满分12分)
一个袋中装有四个现状大小完全相同的球,球的编号分别为1,2,3,4.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求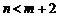 的概率.
的概率.
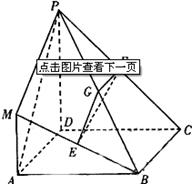 (20)(本小题满分12分)
(20)(本小题满分12分)
在如图所示的几何体中,四边形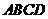 是正方形,
是正方形,
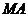
 平面
平面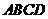 ,
,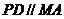 ,
,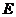 、
、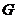 、
、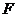 分别为
分别为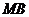 、
、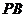 、
、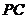 的中点,且
的中点,且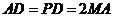 .
.
(I)求证:平面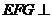 平面
平面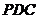 ;
;
(II)求三棱锥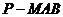 与四棱锥
与四棱锥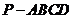 的体积
的体积
之比.
(21)(本小题满分12分)
已知函数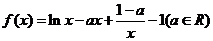
(I)当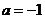 时,求曲线
时,求曲线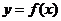 在点
在点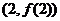 处的切线方程;
处的切线方程;
(II)当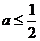 时,讨论
时,讨论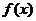 的单调性.
的单调性.
(22)(本小题满分14分)
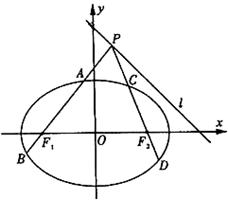 如图,已知椭圆
如图,已知椭圆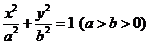 过点.
过点.
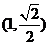 ,离心率为
,离心率为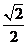 ,左、右焦点分别为
,左、右焦点分别为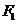 、
、
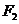 .点
.点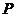 为直线
为直线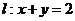 上且不在
上且不在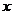 轴上的任意
轴上的任意
一点,直线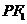 和
和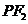 与椭圆的交点分别为
与椭圆的交点分别为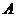 、
、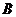
和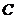 、
、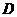 ,
,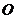 为坐标原点.
为坐标原点.
(I)求椭圆的标准方程;
(II)设直线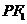 、
、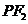 的斜线分别为
的斜线分别为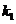 、
、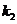 .
.
(i)证明: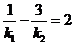 ;
;
(ii)问直线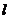 上是否存在点
上是否存在点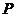 ,使得直线
,使得直线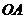 、
、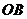 、
、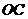 、
、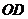 的斜线
的斜线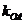 、
、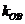 、
、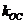 、
、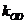 满足
满足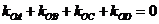 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点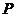 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.






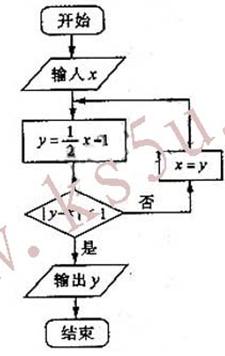
(13)执行右图所示的程序框图,若输入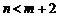
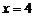 ,则输出y的值为
.
,则输出y的值为
.
(14)已知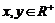 ,且满足
,且满足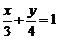 ,则xy的最大值为 .
,则xy的最大值为 .
(15) 在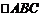 中,角A,B,C所对的边分别为a,b,c,若
中,角A,B,C所对的边分别为a,b,c,若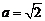 ,
,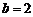 ,
,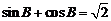 ,则角A的大小为
.
,则角A的大小为
.
(16) 已知圆C过点(1,0),且圆心在x轴的正半轴上,直线l: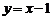 被该圆所截得的弦长为
被该圆所截得的弦长为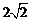 ,则圆C的标准方程为
.
,则圆C的标准方程为
.
(1)
已知全集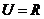 ,集合
,集合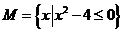 ,则
,则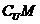 =
=
A. 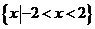 B.
B. 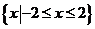
C.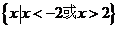 D.
D. 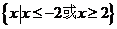
(2)已知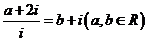 ,其中
,其中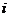 为虚数单位,则
为虚数单位,则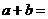
A. 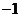 B.
1
C. 2
D. 3
B.
1
C. 2
D. 3
(3)函数 的值域为
的值域为
A.
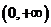 B.
B. 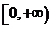 C.
C. 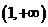 D.
D.
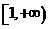
(4)在空间,下列命题正确的是
A.平行直线的平行投影重合
B.平行于同一直线的两个平面平行
C.垂直于同一平面的两个平面平行
D.垂直于同一平面的两条直线平行
(5)设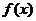 为定义在
为定义在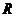 上的奇函数,当
上的奇函数,当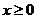 时,
时,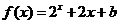 (
(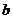 为常数),则
为常数),则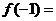
(A)-3 (B)-1 (C)1 (D)3
(6)在某项体育比赛中,七位裁判为一选手打出的分数如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为
(A)92 , 2 (B) 92 , 2.8
(C) 93 , 2 (D) 93 , 2.8
(7)设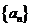 是首项大于零的等比数列,则“
是首项大于零的等比数列,则“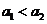 ”是“数列
”是“数列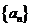 是递增数列”的
是递增数列”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(8)已知某生产厂家的年利润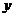 (单位:万元)与年产量
(单位:万元)与年产量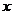 (单位:万件)的幻术关系式为
(单位:万件)的幻术关系式为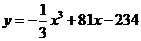 ,则使该生产厂家获得最大年利润的年产量为
,则使该生产厂家获得最大年利润的年产量为
(A)13万件 (B)11万件
(C) 9万件 (D)7万件
(9)已知抛物线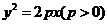 ,过其焦点且斜率为1的直线交抛物线与
,过其焦点且斜率为1的直线交抛物线与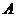 、
、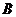 两点,若线段
两点,若线段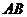 的中点的纵坐标为2,则该抛物线的准线方程为
的中点的纵坐标为2,则该抛物线的准线方程为
(A)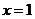 (B)
(B)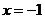
(C)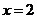 (D)
(D)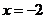
(10)观察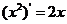 ,
,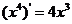 ,
,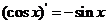 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在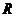 上的函数
上的函数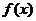 满足
满足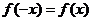 ,记
,记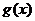 为
为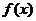 的导函数,则
的导函数,则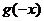 =
=
(A)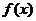 (B)
(B)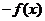 (C)
(C) 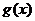 (D)
(D)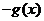
(11)函数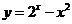 的图像大致是
的图像大致是
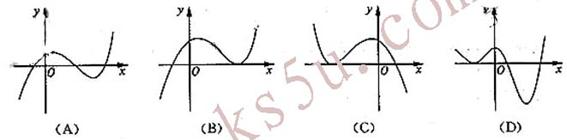
(12)定义平面向量之间的一种运算“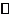 ”如下:对任意的
”如下:对任意的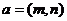 ,
,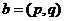 ,令
,令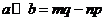 ,下面说法错误的是
,下面说法错误的是
(A)若a与b共线,则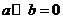
(B)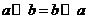
(C)对任意的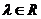 ,有
,有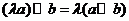
(D)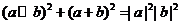
(17)(本小题满分12分)
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为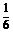 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(Ⅰ)求甲中奖且乙、丙都没有中奖的概率;
(Ⅱ)求中奖人数ξ的分布列及数学期望Eξ.

(18)(本小题满分12分)

 w_w w. k#s5_
w_w w. k#s5_
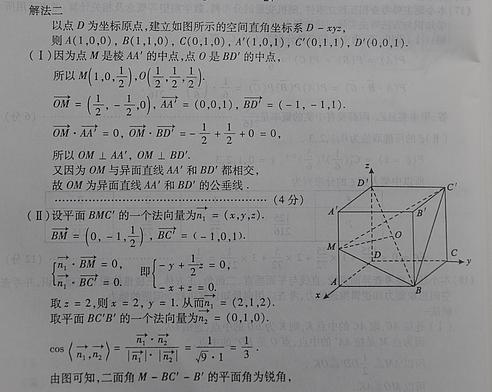
已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点.
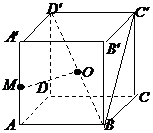 (Ⅰ)求证:OM为异面直线AA'和BD'的公垂线;
(Ⅰ)求证:OM为异面直线AA'和BD'的公垂线;
(Ⅱ)求二面角M-BC'-B'的大小;
(Ⅲ)求三棱锥M-OBC的体积.



(19)(本小题满分12分)
(Ⅰ)1证明两角和的余弦公式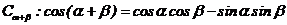 ;
;
2由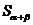 推导两角和的正弦公式
推导两角和的正弦公式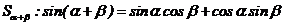 .
.
(Ⅱ)已知△ABC的面积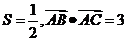 ,且
,且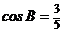 ,求cosC.
,求cosC.

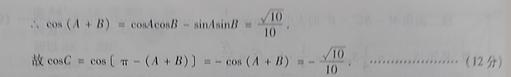
(20)(本小题满分12分)
已知定点A(-1,0),F(2,0),定直线l:x=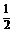 ,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
(Ⅰ)求E的方程;
(Ⅱ)试判断以线段MN为直径的圆是否过点F,并说明理由.

(21)(本小题满分12分)
已知数列{an}满足a1=0,a2=2,且对任意m、n∈N*都有
a2m-1+a2n-1=2am+n-1+2(m-n)2
(Ⅰ)求a3,a5;
(Ⅱ)设bn=a2n+1-a2n-1(n∈N*),证明:{bn}是等差数列;
(Ⅲ)设cn=(an+1-an)qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.

(22)(本小题满分14分)
设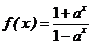 (
(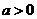 且
且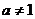 ),g(x)是f(x)的反函数.
),g(x)是f(x)的反函数.
(Ⅰ)设关于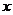 的方程求
的方程求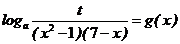 在区间[2,6]上有实数解,求t的取值范围;
在区间[2,6]上有实数解,求t的取值范围;
(Ⅱ)当a=e(e为自然对数的底数)时,证明: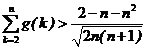 ;
;
(Ⅲ)当0<a≤时,试比较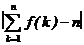 与4的大小,并说明理由.
与4的大小,并说明理由.


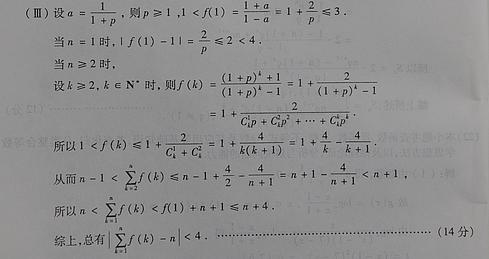


 w_w w. k#s5_
w_w w. k#s5_
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com