
题目列表(包括答案和解析)
1.
设定义在R上的函数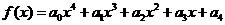 (其中
(其中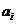 ∈R,i=0,1,2,3,4)
∈R,i=0,1,2,3,4)
当x= -1时,f (x)取得极大值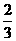 ,并且函数y=f (x+1)的图象关于点(-1,0)对称.
,并且函数y=f (x+1)的图象关于点(-1,0)对称.
(1)求f (x)的表达式;(2)试在函数f
(x)的图象上求两点,使这两点为切点的切线互相垂直,且切点的横坐标都在区间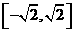 上;(3)若
上;(3)若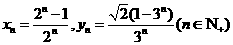 ,求证:
,求证: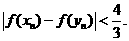
解:(1)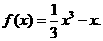 …………………………5分
…………………………5分
(2)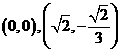 或
或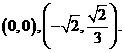 …………10分
…………10分
(3)用导数求最值,可证得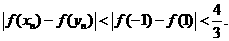 ……15分
……15分
3. 已知数列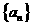 的前n项和为
的前n项和为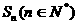 ,且
,且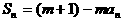 对任意自然数都成立,其中m为常数,且
对任意自然数都成立,其中m为常数,且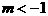 .(I)求证数列
.(I)求证数列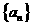 是等比数列;(II)设数列
是等比数列;(II)设数列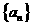 的公比
的公比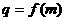 ,数列
,数列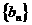 满足:
满足: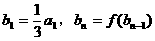
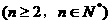 ,试问当m为何值时,
,试问当m为何值时,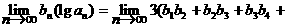
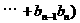 成立?
成立?
解:(I)由已知
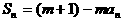 (2)
(2)
由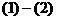 得:
得: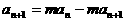 ,即
,即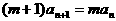 对任意
对任意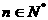 都成立
都成立
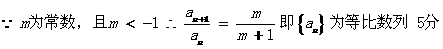
(II)当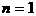 时,
时,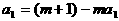
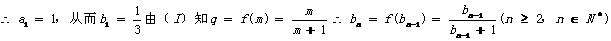
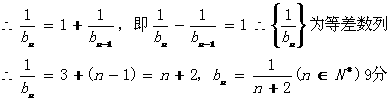
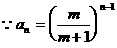 K^S*5U.C#O%
K^S*5U.C#O%
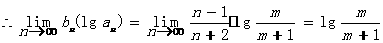
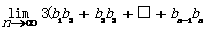
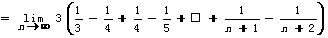 =1
=1
由题意知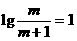 ,
,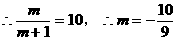 13分
13分
2.垂直于x轴的直线交双曲线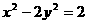 于M、N不同两点,A1、A2分别为双曲线的左顶点和右顶点,设直线A1M与A2N交于点P(x0,y0)K^S*5U.C#O%
于M、N不同两点,A1、A2分别为双曲线的左顶点和右顶点,设直线A1M与A2N交于点P(x0,y0)K^S*5U.C#O%
(Ⅰ)证明: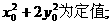 (Ⅱ)过P作斜率为
(Ⅱ)过P作斜率为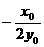 的直线l,原点到直线l的距离为d,求d的最小值.
的直线l,原点到直线l的距离为d,求d的最小值.
解(Ⅰ)证明: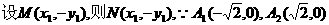
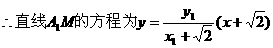 ①直线A2N的方程为
①直线A2N的方程为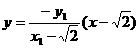 ②…4分
②…4分
①×②,得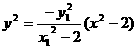
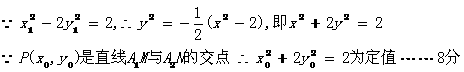
(Ⅱ)
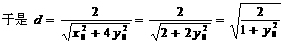 ……10分K^S*5U.C#O%
……10分K^S*5U.C#O%
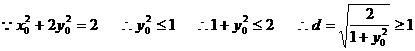
当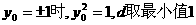 ……12分
……12分
1.已知函数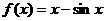
(Ⅰ)若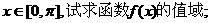
(Ⅱ)若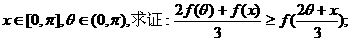
(Ⅲ)若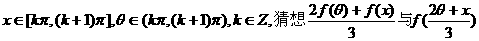 的大小关系(不必写出比较过程).
的大小关系(不必写出比较过程).
解:(Ⅰ)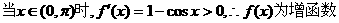
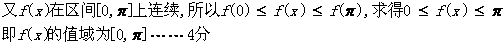
(Ⅱ)设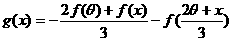 ,
,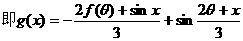
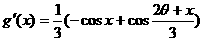 ……6分
……6分
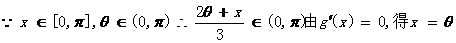
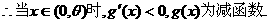
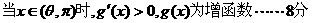
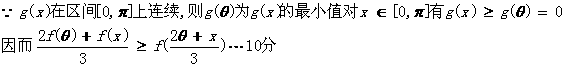
(Ⅲ)在题设条件下,当k为偶数时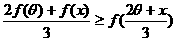 ,当k为奇数时
,当k为奇数时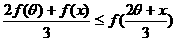 ……4分
……4分
3.已知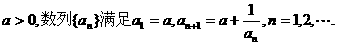
(I)已知数列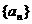 极限存在且大于零,求
极限存在且大于零,求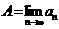 (将A用a表示);(II)设
(将A用a表示);(II)设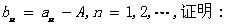
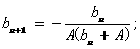 (III)若
(III)若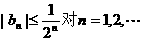 都成立,求a的取值范围.
都成立,求a的取值范围.
解:(I)由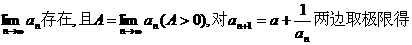
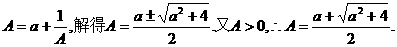
(II)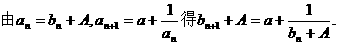
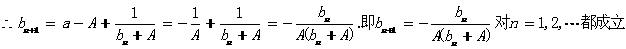
(III)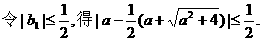
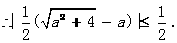
 K^S*5U.C#O
K^S*5U.C#O
(i)当n=1时结论成立(已验证).
(ii)假设当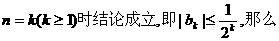
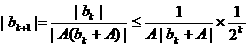
故只须证明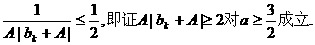 K^S*5U.C#O
K^S*5U.C#O

即n=k+1时结论成立.
根据(i)和(ii)可知结论对一切正整数都成立
故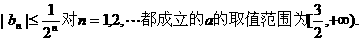
2.如图,P是抛物线C:y=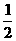 x2上一点,直线l过点P且与抛物线C交于另一点Q.
x2上一点,直线l过点P且与抛物线C交于另一点Q.
(Ⅰ)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求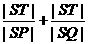 的取值范围.
的取值范围.
本题主要考查直线、抛物线、不等式等基础知识,求轨迹方程的方法,解析几何的基本思想和综合解题能力.满分12分.
解:(Ⅰ)设P(x1,y1),Q(x2,y2),M(x0,y0),依题意x1≠0,y1>0,y2>0.
由y=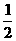 x2, ①得y'=x.∴过点P的切线的斜率k切=
x1,∴直线l的斜率kl=-
x2, ①得y'=x.∴过点P的切线的斜率k切=
x1,∴直线l的斜率kl=-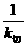 =-
=-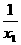
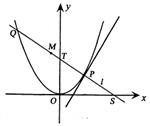 ∴直线l的方程为y-
∴直线l的方程为y-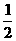 x12=-
x12=-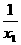 (x-x1),
(x-x1),
方法一:联立①②消去y,得x2+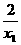 x-x12-2=0.
x-x12-2=0.
∵M是PQ的中点∴x0=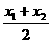 =-
=-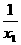 ,y0=
,y0=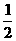 x12-
x12-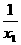 (x0-x1).
(x0-x1).
消去x1,得y0=x02+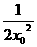 +1(x0≠0),∴PQ中点M的轨迹方程为y=x2+
+1(x0≠0),∴PQ中点M的轨迹方程为y=x2+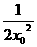 +1(x≠0). K^S*5U.C#O
+1(x≠0). K^S*5U.C#O
方法二:由y1=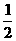 x12,y2=
x12,y2=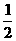 x22,x0=
x22,x0=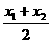 ,得y1-y2=
,得y1-y2=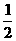 x12-
x12-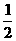 x22=
x22=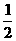 (x1+x2)(x1-x2)=x0(x1-x2),
(x1+x2)(x1-x2)=x0(x1-x2),
则x0=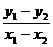 =kl=-
=kl=-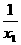 ,∴x1=-
,∴x1=-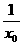 ,将上式代入②并整理,得y0=x02+
,将上式代入②并整理,得y0=x02+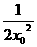 +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+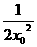 +1(x≠0).
+1(x≠0).
(Ⅱ)设直线l:y=kx+b,依题意k≠0,b≠0,则T(0,b).分别过P、Q作PP'⊥x轴,QQ'⊥y轴,垂足分别为P'、Q',则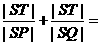
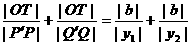 .由y=
.由y=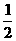 x2
及y=kx+b
消去x,得y2-2(k2+b)y+b2=0. ③则y1+y2=2(k2+b),y1y2=b2.
x2
及y=kx+b
消去x,得y2-2(k2+b)y+b2=0. ③则y1+y2=2(k2+b),y1y2=b2.
方法一:∴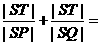 |b|(
|b|(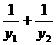 )≥2|b|
)≥2|b|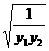 =2|b|
=2|b|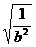 =2.
=2.
∵y1、y2可取一切不相等的正数,∴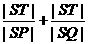 的取值范围是(2,+
的取值范围是(2,+ ).
).
方法二:∴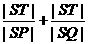 =|b|
=|b|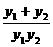 =|b|
=|b|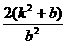 .
.
当b>0时,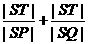 =b
=b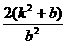 =
=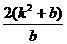 =
=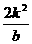 +2>2;
+2>2;
当b<0时,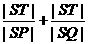 =-b
=-b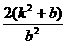 =
=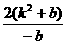 .
.
又由方程③有两个相异实根,得△=4(k2+b)2-4b2=4k2(k2+2b)>0,于是k2+2b>0,即k2>-2b.所以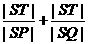 >
>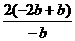 =2.∵当b>0时,
=2.∵当b>0时,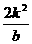 可取一切正数,
可取一切正数,
∴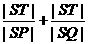 的取值范围是(2,+
的取值范围是(2,+ ).方法三:由P、Q、T三点共线得kTQ=KTP,
).方法三:由P、Q、T三点共线得kTQ=KTP,
即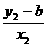 =
=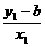 .则x1y2-bx1=x2y1-bx2,即b(x2-x1)=(x2y1-x1y2).于是b=
.则x1y2-bx1=x2y1-bx2,即b(x2-x1)=(x2y1-x1y2).于是b=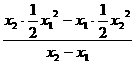 =-
=-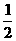 x1x2.
x1x2.
|
|
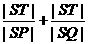 =
=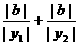 =
=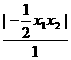 +
+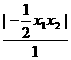 =
=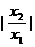 +
+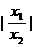 ≥2.
≥2.
∵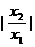 可取一切不等于1的正数,∴
可取一切不等于1的正数,∴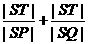 的取值范围是(2,+
的取值范围是(2,+ ).
).
1.已知f(x)=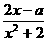 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;(Ⅱ)设关于x的方程f(x)=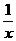 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
解:(Ⅰ)f'(x)=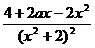 =
=
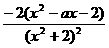 ,
,
∵f(x)在[-1,1]上是增函数,∴f'(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立. ①
设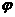 (x)=x2-ax-2,
(x)=x2-ax-2,
方法一: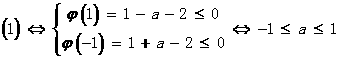
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
方法二: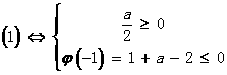 或
或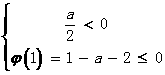
 0≤a≤1或-1≤a≤0
0≤a≤1或-1≤a≤0 -1≤a≤1.
-1≤a≤1.
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
(Ⅱ)由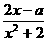 =
=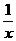 ,得x2-ax-2=0, ∵△=a2+8>0
,得x2-ax-2=0, ∵△=a2+8>0
∴x1,x2是方程x2-ax-2=0的两非零实根, x1+x2=a,x1x2=-2,
∴
从而|x1-x2|=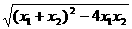 =
=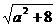 .
.
∵-1≤a≤1,∴|x1-x2|=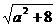 ≤3. K^S*5U.C#O
≤3. K^S*5U.C#O
要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,即m2+tm-2≥0对任意t∈[-1,1]恒成立. ②
设g(t)=m2+tm-2=mt+(m2-2),
方法一:
② g(-1)=m2-m-2≥0且g(1)=m2+m-2≥0 m≥2或m≤-2. 所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
m≥2或m≤-2. 所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
方法二:当m=0时,②显然不成立;K^S*5U.C#O
当m≠0时,② m>0且 g(-1)=m2-m-2≥0或m<0且g(1)=m2+m-2≥0
m>0且 g(-1)=m2-m-2≥0或m<0且g(1)=m2+m-2≥0 m≥2或m≤-2.所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
m≥2或m≤-2.所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
3.已知数列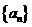 中,
中,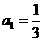 ,当
,当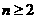 时,其前
时,其前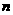 项和
项和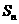 满足
满足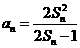 ,
,
(1)求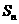 的表达式及
的表达式及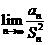 的值;(2)求数列
的值;(2)求数列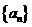 的通项公式;(3)设
的通项公式;(3)设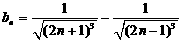 ,求证:当
,求证:当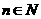 且
且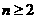 时,
时,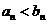 .
.
解:(1)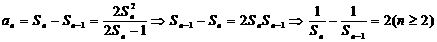
所以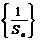 是等差数列.则
是等差数列.则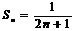 .
.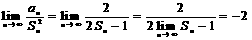 .
.
(2)当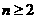 时,
时,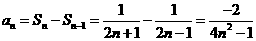 ,综上,
,综上,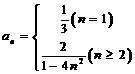 .
.
(3)令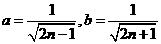 ,当
,当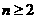 时,有
时,有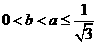 (1)
(1)
法1:等价于求证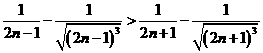 .
.
当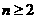 时,
时,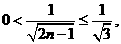 令
令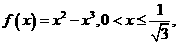
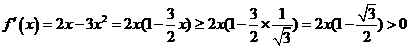 ,则
,则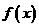 在
在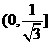 递增.
递增.
又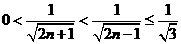 ,所以
,所以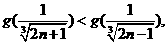 即
即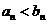 .
.
法(2)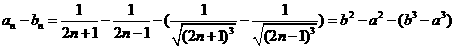
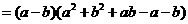 (2)K^S*5U.C#O%
(2)K^S*5U.C#O%
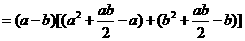
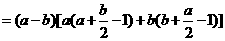 (3)
(3)
因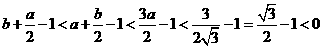 ,所以
,所以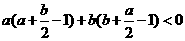
由(1)(3)(4)知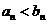 . K^S*5U.C#O%
. K^S*5U.C#O%
法3:令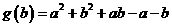 ,则
,则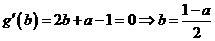
所以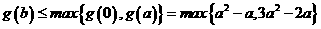
因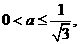 则
则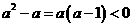 ,
,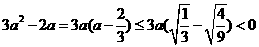
所以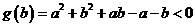 (5)
(5)
由(1)(2)(5)知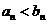
2.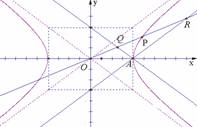 设双曲线
设双曲线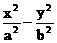 =1( a > 0, b > 0 )的右顶点 为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP分别交于Q和R两点
=1( a > 0, b > 0 )的右顶点 为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP分别交于Q和R两点
(1) 证明:无论P点在什么位置,总有|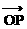 |2 = |
|2 = |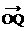 ·
·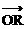 | ( O为坐标原点);
| ( O为坐标原点);
(2) 若以OP为边长的正方形面积等于双曲线实、虚轴围成的矩形面积,求双曲线离心率的取值范围;
解:(1) 设OP:y = k x, 又条件可设AR: y = 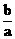 (x – a ),
(x – a ),
解得: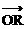 = (
= (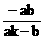 ,
,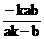 ), 同理可得
), 同理可得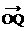 = (
= (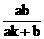 ,
,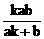 ),
),
∴|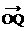 ·
·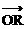 | =|
| =|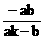
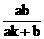 +
+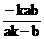
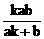 | =
| =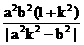 . 4分
. 4分
设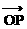 = ( m, n ) , 则由双曲线方程与OP方程联立解得m2 =
= ( m, n ) , 则由双曲线方程与OP方程联立解得m2 =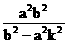 , n2 =
, n2 = 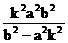 ,
,
∴ |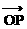 |2 = :m2 + n2 =
|2 = :m2 + n2 = 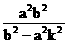 +
+ 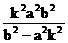 =
=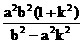 ,
,
∵点P在双曲线上,∴b2 – a2k2 > 0 . ∴无论P点在什么位置,总有|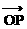 |2 = |
|2 = |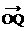 ·
·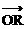 | . 4分K^S*5U.C#O%
| . 4分K^S*5U.C#O%
(2)由条件得: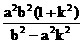 = 4ab, 2分
= 4ab, 2分
即k2 = 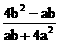 > 0 , ∴ 4b > a, 得e >
> 0 , ∴ 4b > a, 得e > 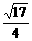 2分
2分
1. 已知常数a > 0, n为正整数,f n ( x ) = x n – ( x + a)n ( x > 0 )是关于x的函数.
(1) 判定函数f n ( x )的单调性,并证明你的结论.
(2) 对任意n ³ a , 证明f `n + 1 ( n + 1 ) < ( n + 1 )fn`(n)
解: (1) fn `( x ) = nx n – 1 – n ( x + a)n – 1 = n [x n – 1 – ( x + a)n – 1 ] ,
∵a > 0 , x > 0, ∴ fn `( x ) < 0 , ∴ f n ( x )在(0,+∞)单调递减. 4分
(2)由上知:当x > a>0时, fn ( x ) = xn – ( x + a)n是关于x的减函数,
∴ 当n ³ a时, 有:(n + 1 )n– ( n + 1 + a)n £ n n – ( n + a)n. 2分
又 ∴f `n + 1 (x ) = ( n + 1 ) [xn –( x+ a )n ] ,
∴f `n + 1( n+1) = (n+1)[(n +1)n –(n +1+a)n]<(n+1)[nn–(n+a)n]=(n+1)[nn–(n+a)(n+a)n–1] 2分
( n + 1 )fn`(n) = ( n + 1 )n[n n – 1 – ( n + a)n – 1 ] = ( n + 1 )[n n – n( n + a)n – 1 ], 2分
∵( n + a ) > n ,∴f `n + 1 ( n + 1 ) < ( n + 1 )fn`(n) . 2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com