
题目列表(包括答案和解析)
(17)(本小题满分12分)
已知函数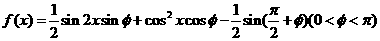 ,其图像过点
,其图像过点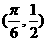 。
。
(Ⅰ) 求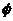 的值;
的值;
(Ⅱ) 将函数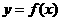 的图像上各点的横坐标缩短到原来的
的图像上各点的横坐标缩短到原来的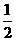 ,纵坐标不变,得到函数
,纵坐标不变,得到函数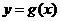 的图像,求函数
的图像,求函数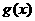 在
在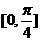 上的最大值和最小值。
上的最大值和最小值。
(18)(本小题满分12分)
已知等差数列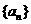 满足:
满足: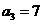 ,
,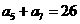 ,
,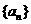 的前n项和为
的前n项和为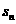 。
。
(Ⅰ) 求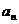 及
及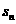 ;
;
(Ⅱ) 令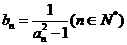 ,求数列
,求数列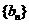 的前n项和
的前n项和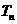 。
。
(19)(本小题满分12分)
如图,在无棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45。
。AB=2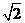 ,BC=2AE=4,三角形PAB是等腰三角形。
,BC=2AE=4,三角形PAB是等腰三角形。
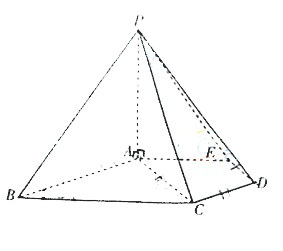
(Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅱ)求直线PB与平面PCD所成角的大小;
(Ⅲ)求四棱锥P-ACDE的体积。
(20)(本小题满分12分)
某学校举行知识竞赛,第一轮选拔共设有A、B、C、D四个问题,规则如下:
① 每位参加者记分器的初始分均为10分,答对问题A、B、C、D分别加1分、2分、3分、6分,答错任一题减2分;
② 每回答一题,记分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
③ 每位参加者按问题A、B、C、D顺序作答,直至答题结束。
假设甲同学对问题A、B、C、D回答正确的概率依次为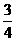 、
、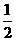 、
、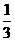 、
、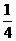 ,且各题回答正确与否相互之间没有影响。
,且各题回答正确与否相互之间没有影响。
(Ⅰ)求甲同学能进入下一轮的概率;
(Ⅱ)用ξ表示甲同学本轮答题结束时答题的个数,求ξ的分布列和数学期望Εξ。
21.(本小题满分12分)
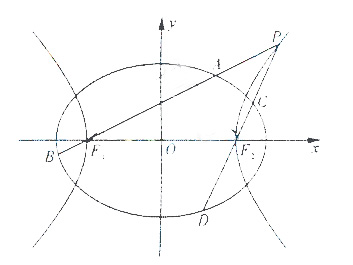
如图,已知椭圆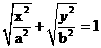 (a>b>0)的离心率为
(a>b>0)的离心率为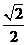 ,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为
,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为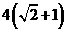 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
(Ⅰ)求椭圆和双曲线的标准方程
(Ⅱ)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1
(Ⅲ)是否存在常数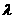 ,使得|AB|+|CD|=
,使得|AB|+|CD|=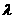 |AB|·|CD|恒成立?若存在,求
|AB|·|CD|恒成立?若存在,求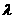 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(22)(本小题满分14分)
已知函数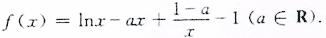
(Ⅰ)当a≤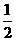 时,讨论f(x)的单调性:
时,讨论f(x)的单调性:
(Ⅱ)设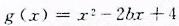 .当a=
.当a=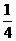 时,若对任意x1∈(0,2),存在x2∈
时,若对任意x1∈(0,2),存在x2∈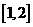 ,使
,使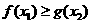 ,求实数b的取值范围。
,求实数b的取值范围。
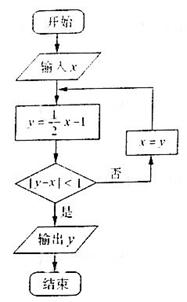 (13)执行右图所示的程序框图,若输入
(13)执行右图所示的程序框图,若输入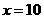 ,则输出
,则输出
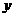 的值为
。
的值为
。
(14)若对任意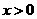 ,
,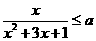 恒成立,则
恒成立,则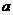 的
的
取值范围是 。
(15)在△ABC中,角A,B,C所对的边分别为a,b,c,若a=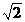 ,b=2,sinB+cosB=
,b=2,sinB+cosB=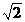 ,则角A的大小为______________.
,则角A的大小为______________.
(16)已知圆C过点(1,0),且圆心在x轴的正半轴上,直线l:y=x-1被圆C所截得的弦长为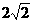 ,则过圆心且与直线l垂直的方程为_______________.
,则过圆心且与直线l垂直的方程为_______________.
(11)设A=|x|x+1>0|,B=|x|x<0|,则A∩B=
(12)已知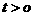 ,则函数
,则函数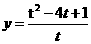 的最小值为
的最小值为
 (13)已知过抛物线y2=4x的焦点F的直线交该抛物线于A、B两点,|AF|=2,则|BF|=
(13)已知过抛物线y2=4x的焦点F的直线交该抛物线于A、B两点,|AF|=2,则|BF|=
(14)加工某一零件经过三道工序,设第一、二、三道工序的次品率分别为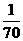 、
、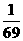 、
、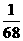 ,且各道工序互不影响,则加工出来的零件的次品率为
。
,且各道工序互不影响,则加工出来的零件的次品率为
。
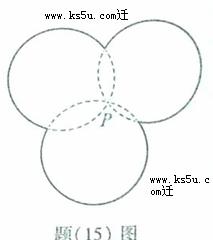
(15)如题(15)图,图中的实线是由三段圆弧连接而成的一条封闭曲线C,各段弧所在的圆经过同一点P(点P不在C上)且半径相等。设第i段弧所对的圆心角为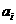 (i=1,2,3),则
(i=1,2,3),则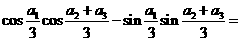
三 解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
(16)(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)
已知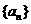 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,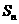 为
为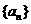 的前n项和。
的前n项和。
(Ⅰ)求通向公式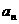 及
及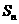 ;
;
(Ⅱ)设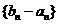 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列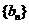 的通向公式及其前n项和
的通向公式及其前n项和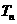
(17) (本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)
在甲、乙等6个单位参加的一次“唱读讲传”演出活动中,每个单位的节目集中安排在一起.若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……6),求:
(Ⅰ)甲、乙两单位的演出序号均为偶数的概率;
(Ⅱ)甲、乙两单位的演出序号不相邻的概率.
(18)(本小题满分13分。(Ⅰ)小问5分,(Ⅱ)小问8分.)
设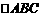 的内角A、B、C的对边长分别为a、b、c,且
的内角A、B、C的对边长分别为a、b、c,且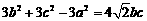 .
.
(Ⅰ)求 的值.
的值.
(Ⅱ)求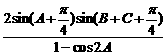 的值.
的值.
(19)(本小题满分12分。(Ⅰ)小问5分,(Ⅱ)小问7分.)
已知函数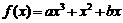 (其中常数a,b∈R),
(其中常数a,b∈R),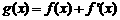 是奇函数.
是奇函数.
(Ⅰ)求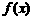 的表达式;
的表达式;
(Ⅱ)讨论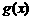 的单调性,并求
的单调性,并求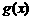 在区间
在区间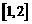 上的最大值与最小值.
上的最大值与最小值.
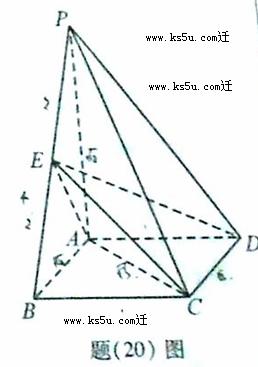
(20)(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分.)
如题(20)图,四棱柱P-ABCD中,底面ABCD为矩形,PA底面
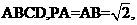 点E是棱PB的中点。
点E是棱PB的中点。
( Ⅰ)证明:AE⊥平面PBC
(Ⅱ)若AD=1,求二面角B-EC-D的平面角的余弦值。
(21 )(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分。)
已知以原点O为中心,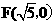 为右焦点的双曲线c的离心率
为右焦点的双曲线c的离心率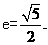
(Ⅰ)球双曲线c的标准方程及其渐近线方程;
(Ⅱ)如题(21 )图,已知过点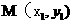 的直线:
的直线: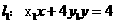 与过点
与过点
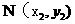
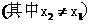 的直线
的直线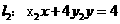 的交点在双曲线c上,
的交点在双曲线c上,
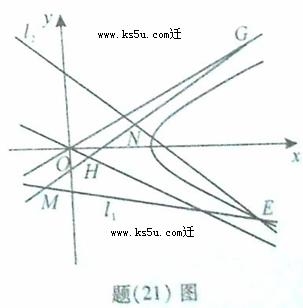
直线MN与双曲线的两条渐近线分别交与G、H两点,求的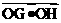 值。
值。
(1)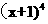 的展开式中
的展开式中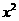 的系数为
的系数为
(A)4 (B) 6 (C) 10 (D) 20
(2) 在等差数列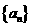 中,则
中,则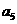 的值为
的值为
(A)5 (B) 6 (C) 8 (D) 10
(3) 若向量a=(3,m),b=(2,-1),a·b=0,则实数m的值为
(A)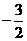 (B)
(B) 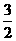 (C) 2
(D) 6
(C) 2
(D) 6
(4)函数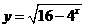 的值域是
的值域是
(A)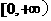 (B)
(B) 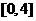 (C)
(C) 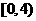 (D)
(D) 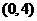
(5)某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本中的青年职工为7人,则样本容量为
(A)7 (B)15
(C)25 (D)35
(6)下列函数中,周期为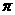 ,且在
,且在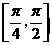 上为减函数的是
上为减函数的是
(A)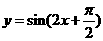 (B)
(B)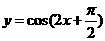
(C)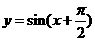 (D)
(D)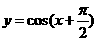
(7)设变量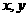 满足约束条件
满足约束条件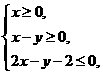 则
则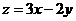 的最大值为
的最大值为
(A)0 (B)2
(C)4 (D)6
(8)若直线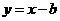 与曲线
与曲线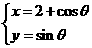 ,(
,(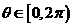 )有两个不同的公共点,则实数
)有两个不同的公共点,则实数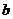 的取值范围为
的取值范围为
(A)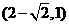 (B)
(B)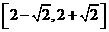
(C)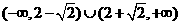 (D)
(D)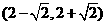
(9)到两互相垂直的异面直线的距离相等的点
(A)只有1个 (B)恰有3个
(C)恰有4个 (D)有无穷多个
(10)某单位拟安排6位员工在今年6月14日至16日(端午节假期)值班,每天安排2人,每人值班1天。若6位员工中的甲不值14日,乙不值16日,则不同的安排方法共有
(A)30种 (B)36种 (C)42种 (D)48种
20.解:(1)由: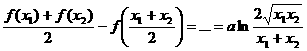 ,
,
而: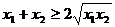
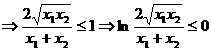 ,
,
又因为: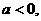 所以:
所以: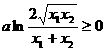 ,即:
,即: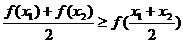 成立。
成立。
(2) 由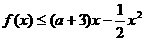 恒成立,即只要:
恒成立,即只要: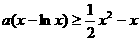 成立;
成立;
又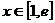 ,易知
,易知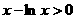
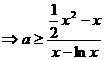
令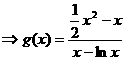 (
(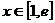 )
)
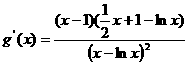 ,令:
,令: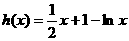 ,
,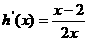
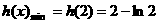
 ,
,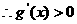
所以: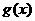 在
在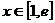 上为增函数。
上为增函数。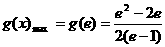
即: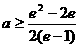
20.(16分)已知函数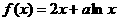 。
。
(1)若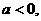 证明:对于任意的两个正数
证明:对于任意的两个正数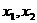 ,总有
,总有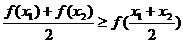 成立;
成立;
(2)若对任意的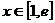 ,不等式:
,不等式: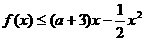 恒成立,求
恒成立,求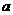 的取值范围。
的取值范围。
19.解 (Ⅰ)设需要新建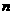 个桥墩,
个桥墩,
所以 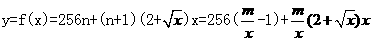
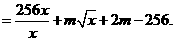
(Ⅱ) 由(Ⅰ)知,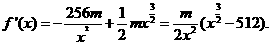
令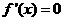 ,得
,得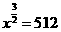 ,所以
,所以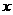 =64
=64
当0<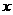 <64时
<64时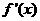 <0,
<0, 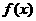 在区间(0,64)内为减函数;
在区间(0,64)内为减函数;
当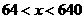 时,
时,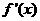 >0.
>0. 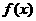 在区间(64,640)内为增函数,
在区间(64,640)内为增函数,
所以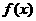 在
在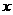 =64处取得最小值,此时,
=64处取得最小值,此时,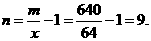
故需新建9个桥墩才能使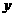 最小。
最小。
19.某地建一座桥,两端的桥墩已建好,这两墩相距 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为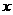 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为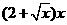 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为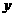 万元。
万元。
(Ⅰ)试写出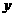 关于
关于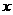 的函数关系式;
的函数关系式;
(Ⅱ)当 =640米时,需新建多少个桥墩才能使
=640米时,需新建多少个桥墩才能使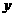 最小?(16分)
最小?(16分)
18.解:(1)椭圆的标准方程: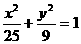 ;
;
(2)设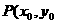 ),则
),则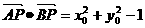 ;
;
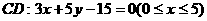
则当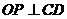 时,取到最小值,即:
时,取到最小值,即: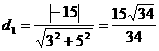 ;
;
当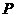 在
在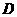 点时,取到最大值:
点时,取到最大值: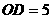
所以: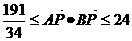 。
。
(3)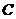 上存在点
上存在点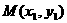 使
使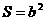 的充要条件是:
的充要条件是: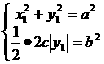
易得:当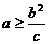 时存在点M使得:
时存在点M使得: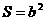
此时:
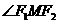 =2。
=2。
18.(15分)已知椭圆以坐标原点为中心,坐标轴为对称轴,且椭圆以抛物线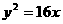 的焦点为其一个焦点,以双曲线
的焦点为其一个焦点,以双曲线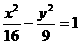 的焦点为顶点。
的焦点为顶点。
(1)求椭圆的标准方程;
(2)已知点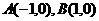 ,且
,且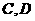 分别为椭圆的上顶点和右顶点,点
分别为椭圆的上顶点和右顶点,点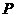 是线段
是线段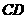 上的动点,求
上的动点,求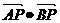 的取值范围。
的取值范围。
(3)试问在圆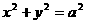 上,是否存在一点
上,是否存在一点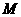 ,使
,使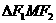 的面积
的面积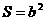 (其中
(其中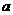 为椭圆的半长轴长,
为椭圆的半长轴长,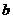 为椭圆的半短轴长,
为椭圆的半短轴长,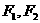 为椭圆的两个焦点),若存在,求
为椭圆的两个焦点),若存在,求
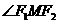 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com