
题目列表(包括答案和解析)
5.已知正项等比数列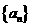 满足:
满足: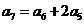 ,若存在两项
,若存在两项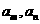 使得
使得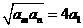 ,则
,则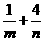 的最小值为( )
的最小值为( )
A. 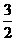 B.
B. 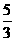 C.
C. 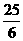 D. 不存在
D. 不存在
4.函数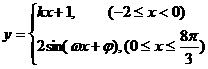 的图象如下图,则( )
的图象如下图,则( )
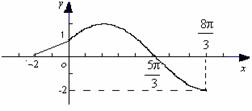 A.
A.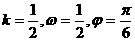 B.
B.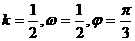
C.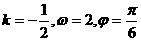
D.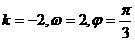
3.有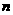 个小球,将它们任意分成两堆,求出这两堆小球球数的乘积,再将其中一堆小球任意分成两堆,求出这两堆小球球数的乘积,如此下去,每次都任选一堆,将这堆小球任意分成两堆,求出这两堆小球球数的乘积,直到不能再分为止,则所有乘积的和为( ).
个小球,将它们任意分成两堆,求出这两堆小球球数的乘积,再将其中一堆小球任意分成两堆,求出这两堆小球球数的乘积,如此下去,每次都任选一堆,将这堆小球任意分成两堆,求出这两堆小球球数的乘积,直到不能再分为止,则所有乘积的和为( ).
( )
)
 (
( )
)
 (
( )
)
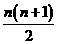 (
( )
)
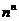
2.长度分别为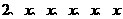 的六条线段能成为同一个四面体的六条棱的充要条件是( ).
的六条线段能成为同一个四面体的六条棱的充要条件是( ).
( )
)
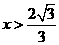 (
( )
)
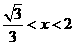 (
(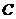 )
)
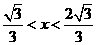 (
(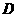 )
)
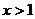
1.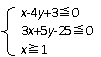 已知点P(x,y)的坐标满足
,设A (2,0)则
已知点P(x,y)的坐标满足
,设A (2,0)则 ·
·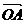 (O为坐标原点)的最大值为
(O为坐标原点)的最大值为
A.5 B.10 C.12 D.15
3.已知函数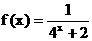
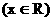 .
.
(1) 试证函数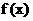 的图象关于点
的图象关于点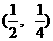 对称;(2) 若数列
对称;(2) 若数列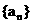 的通项公式为
的通项公式为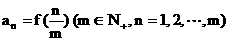 , 求数列
, 求数列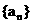 的前m项和
的前m项和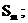 (3) 设数列
(3) 设数列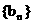 满足:
满足: 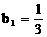 ,
,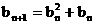 .设
.设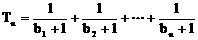 ,若(2)中的
,若(2)中的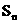 满足对任意不小于2的正整数n,
满足对任意不小于2的正整数n,
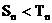 恒成立, 试求m的最大值.
恒成立, 试求m的最大值.
解: (1)设点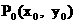 是函数
是函数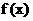 的图象上任意一点, 其关于点
的图象上任意一点, 其关于点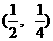 的对称点为
的对称点为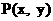 .由
.由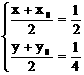 得
得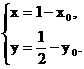 所以, 点P的坐标为P
所以, 点P的坐标为P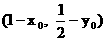 .………………(2分)
.………………(2分)
由点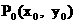 在函数
在函数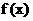 的图象上, 得
的图象上, 得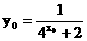 .
.
∵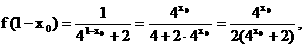
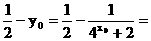
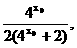 ∴点P
∴点P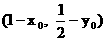 在函数
在函数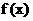 的图象上.
的图象上.
∴函数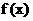 的图象关于点
的图象关于点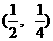 对称. ………………(4分)
对称. ………………(4分)
(2)由(1)可知, 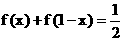 , 所以
, 所以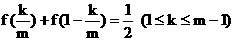 ,
,
即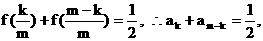 ………………(6分)
………………(6分)
由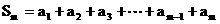 , ……
①得
, ……
①得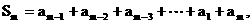 ……②K^S*5U.C#O
……②K^S*5U.C#O
由①+②, 得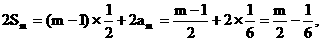
∴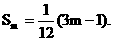 ……… (8分)
……… (8分)
(3) ∵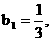
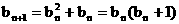 ③∴对任意的
③∴对任意的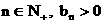 . …④
. …④
由③、④, 得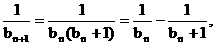 即
即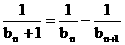 .
.
∴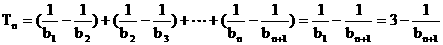 .……(10分)
.……(10分)
∵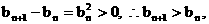 ∴数列
∴数列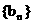 是单调递增数列
是单调递增数列
∴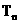 关于n递增. 当
关于n递增. 当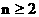 , 且
, 且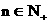 时,
时, 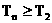 .
.
∵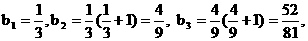
∴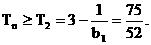 ………………(12分) K^S*5U.C#O
………………(12分) K^S*5U.C#O
∴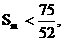 即
即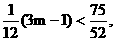 ∴
∴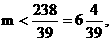 ∴m的最大值为6. ………(14分)
∴m的最大值为6. ………(14分)

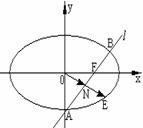
2.将圆O: 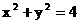 上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线C
上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线C
(1) 求C的方程(2)
设O为坐标原点, 过点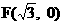 的直线l与C交于A、B两点, N为线段AB的中点,延长线段ON交C于点E.求证:
的直线l与C交于A、B两点, N为线段AB的中点,延长线段ON交C于点E.求证: 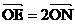 的充要条件是
的充要条件是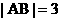 .
.
解: (1)设点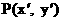 , 点M的坐标为
, 点M的坐标为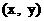 ,由题意可知
,由题意可知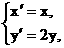 ………………(2分)
………………(2分)
又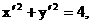 ∴
∴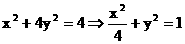 .
.
所以, 点M的轨迹C的方程为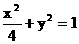 .………………(4分)
.………………(4分)
(2)设点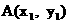 ,
, 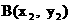 , 点N的坐标为
, 点N的坐标为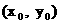 ,
,
㈠当直线l与x轴重合时, 线段AB的中点N就是原点O, 不合题意,舍去; ………(5分)
㈡设直线l: 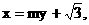 由
由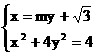 消去x, 得
消去x, 得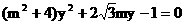 ……①
……①
 ∴
∴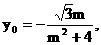 ………………(6分)
………………(6分)
∴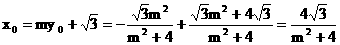 ,
,
∴点N的坐标为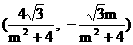 .………………(8分)
.………………(8分)
①若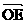
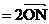 , 坐标为, 则点E的为
, 坐标为, 则点E的为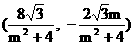 , 由点E在曲线C上,
, 由点E在曲线C上,
得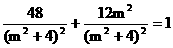 , 即
, 即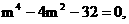 ∴
∴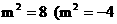 舍去).
舍去).
由方程①得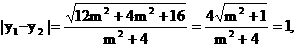
又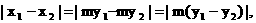 ∴
∴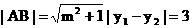 .… (10分)
.… (10分)
②若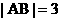 , 由①得
, 由①得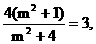 ∴
∴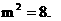 K^S*5U.C#O
K^S*5U.C#O
∴点N的坐标为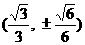 , 射线ON方程为:
, 射线ON方程为: 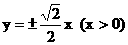 ,
,
由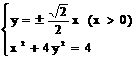 解得
解得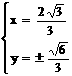 ∴点E的坐标为
∴点E的坐标为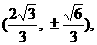 ∴
∴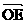
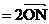 .
.
综上, 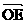
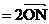 的充要条件是
的充要条件是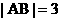 .………………(12分)
.………………(12分)
1.已知函数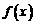 和
和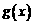 的图象关于原点对称,且
的图象关于原点对称,且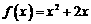 .
.
(Ⅰ)求函数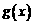 的解析式; (Ⅱ)解不等式
的解析式; (Ⅱ)解不等式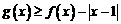 ;
;
(Ⅲ)若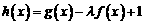 在
在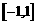 上是增函数,求实数
上是增函数,求实数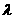 的取值范围.
的取值范围.
本题主要考查函数图象的对称、二次函数的基本性质与不等式的应用等基础知识,以及综合运用所学知识分析和解决问题的能力.
解:(Ⅰ)设函数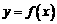 的图象上任意一点
的图象上任意一点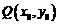 关于原点的对称点为
关于原点的对称点为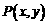 ,则
,则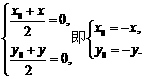
∵点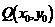 在函数
在函数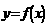 的图象上∴
的图象上∴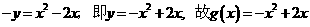
(Ⅱ)由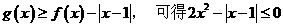
当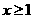 时,
时,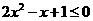 ,此时不等式无解;当
,此时不等式无解;当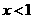 时,
时,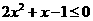 ,解得
,解得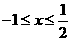 .
.
因此,原不等式的解集为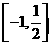 . K^S*5U.C#O
. K^S*5U.C#O
(Ⅲ)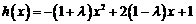
①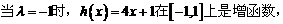
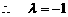
②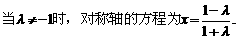
ⅰ)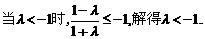 ⅱ)
ⅱ)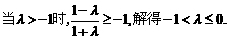
3.已知数列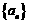 各项均不为0,其前
各项均不为0,其前 项和为
项和为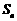 ,且对任意
,且对任意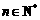 都有
都有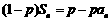 (
(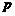 为大于1的常数),记
为大于1的常数),记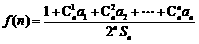 . K^S*5U.C#O
. K^S*5U.C#O
(1) 求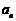 ;(2) 试比较
;(2) 试比较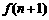 与
与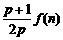 的大小(
的大小(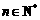 );
);
(3) 求证: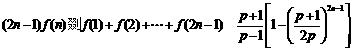 ,(
,(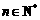 ).
).
解:(1) ∵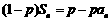 , ① ∴
, ① ∴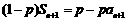 .②
.②
②-①,得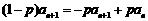 ,即
,即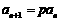 . (3分)
. (3分)
在①中令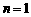 ,可得
,可得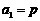 .∴
.∴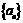 是首项为
是首项为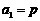 ,公比为
,公比为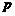 的等比数列,
的等比数列,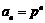 (4分)
(4分)
(2) 由(1)可得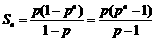 .
.
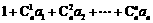
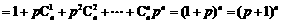 .
.
∴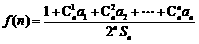
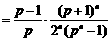 ,(5分)
,(5分)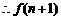
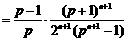 .
.
而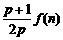
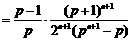 ,且
,且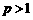 ,
,
∴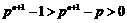 ,
,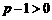 .∴
.∴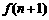

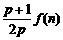 ,(
,(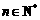 ). (8分)
). (8分)
(3) 由(2)知 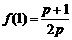 ,
,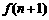

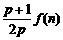 ,(
,(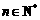 ).
).
∴当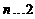 时,
时,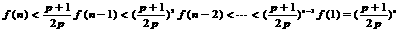 .
.
∴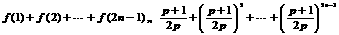
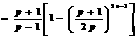 (10分)
(10分)
(当且仅当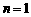 时取等号). K^S*5U.C#O
时取等号). K^S*5U.C#O
另一方面,当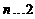 ,
,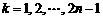 时,
时,

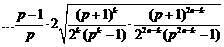
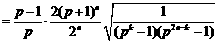
 .
.
∵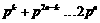 ,∴
,∴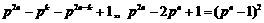 .
.
∴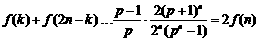 ,(当且仅当
,(当且仅当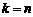 时取等号).(13分)
时取等号).(13分)
∴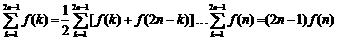 .(当且仅当
.(当且仅当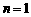 时取等号).
时取等号).
综上所述,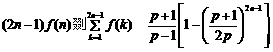 ,(
,(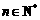 ).(14分)
).(14分)
2.过抛物线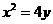 上不同两点A、B分别作抛物线的切线相交于P点,
上不同两点A、B分别作抛物线的切线相交于P点,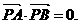
(1)求点P的轨迹方程;(2)已知点F(0,1),是否存在实数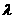 使得
使得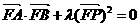 ?若存在,求出
?若存在,求出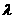 的值,若不存在,请说明理由. K^S*5U.C#O
的值,若不存在,请说明理由. K^S*5U.C#O
解法(一):(1)设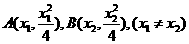 由
由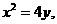 得:
得: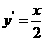
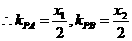
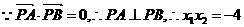 ………………………3分
………………………3分
直线PA的方程是: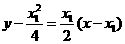 即
即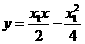 ①
①
同理,直线PB的方程是: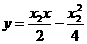 ②
②
由①②得: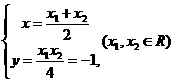 ∴点P的轨迹方程是
∴点P的轨迹方程是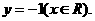 ………6分
………6分
(2)由(1)得: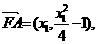
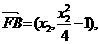
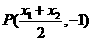
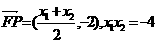
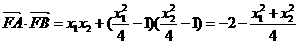 …………………………10分
…………………………10分
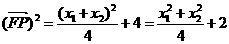 所以
所以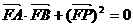
故存在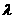 =1使得
=1使得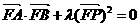 …………………………12分
…………………………12分
解法(二):(1)∵直线PA、PB与抛物线相切,且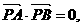
∴直线PA、PB的斜率均存在且不为0,且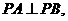
设PA的直线方程是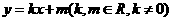 由
由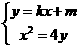 得:
得: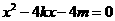
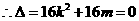 即
即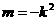 ……………3分
……………3分
即直线PA的方程是: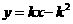 .同理可得直线PB的方程是:
.同理可得直线PB的方程是: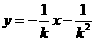
由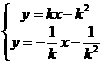 得:
得: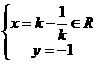 故点P的轨迹方程是
故点P的轨迹方程是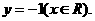 …………6分
…………6分
(2)由(1)得: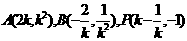
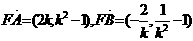 ,
,
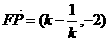
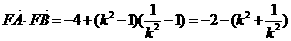 ………10分
………10分
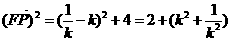 故存在
故存在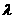 =1使得
=1使得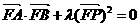 ……12分
……12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com